Eksponentiel funktionsdefinition

Hæmning Strengteori / by admin / April 02, 2023

Marco Antonio Rodriguez Andrade
Master of Mathematics, Dr. of Science

Den eksponentielle funktion modellerer forskellige naturfænomener og sociale og økonomiske situationer, hvorfor det er vigtigt at identificere eksponentielle funktioner i forskellige sammenhænge.

Lad os huske, at for et tal er ${a^1} = a,{a^2} = aa,\;{a^3} = aaa$ defineret, generelt har vi det for enhver \(n\ ) tal naturligt:

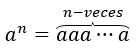
I tilfælde af $a \ne 0$, har vi det: ${a^0} = 1,\;$ faktisk, når $a \ne 0,$ giver det mening at udføre operationen \ (\frac{a}{a} = 1;\) når vi anvender eksponentloven, har vi:

$\frac{a}{a} = 1$

${a^{1 – 1}} = 1$

${a^0} = 1.$

Når $a = 0$, giver den tidligere begrundelse ikke mening, derfor mangler udtrykket ${0^0},$ en matematisk fortolkning.

I tilfælde af, at $b > 0$ og det er rigtigt, at ${b^n} = a,$ siges det, at $b$ er den n'te rod af $a$ og er normalt angivet som \ (b = {a^{\frac{1}{n}}},\;\) eller $b = \sqrt[n]{a}$.

Når $a < 0$, er der ikke noget reelt tal $b$, således at ${b^2} = a;$ fordi ${b^2} \ge 0;\;\ ) så formens udtryk \({a^{\frac{m}{n}}}$, vil ikke blive taget i betragtning for $a < 0.$ I følgende algebraiske udtryk: ${a^n}$ $a \ ) kaldes base, og \(n$ er kaldet eksponent, ${a^n}$kaldes potensen$\;n$ af $a$ eller kaldes også $a$ i potensen $n,\;$se overholde følgende love af eksponenterne:

instagram story viewer

${a^n}{a^m} = {a^{n + m}}$	$\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}$	${\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}$
$\frac{1}{{{a^n}}} = {a^{ – n}}$	${a^n} = \frac{1}{{{a^{ – n}}}}$	${\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}$
${\left( {ab} \right)^n} = {a^n}{b^n}$	${\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}$	${a^0} = 1$ for hver $a \ne 0$

Den eksponentielle funktion har formen:

$f\venstre( x \højre) = {a^x}$

hvor $a > 0$ er en konstant, og den uafhængige variabel er eksponenten $x$.

For at lave en analyse af den eksponentielle funktion vil vi overveje tre tilfælde

Tilfælde 1 Når grundtallet $a = 1.$

I dette tilfælde er $a = 1,$ funktionen $f\venstre( x \right) = {a^x}$ en konstant funktion.

Tilfælde 2 Når grundlaget $a > 1$

I dette tilfælde har vi følgende:

Værdien af $x$
$x < 0$	$0 < {a^x} < 1$
$x = 0$	${a^0} = 1$
$0 < x < 1$	$1 < {a^x} < a$
$x = 1$	${a^x} = 1$
$x > 1$	$a < {a^x}$

Funktionen $f\left( x \right) = {a^x}$ er en strengt stigende funktion, det vil sige, hvis ${x_2} > {x_1}$, så:

${a^{{x_2}}} > a_{}^{{x_2}}$

$f\left( {{x_2}} \right) > f\left( {{x_1}} \right)$

Når et fænomen modelleres med en eksponentiel funktion, med $a > 1$, siger vi, at det præsenterer eksponentiel vækst.

Tilfælde 2 Når grundlaget $a < 1$.

Værdien af $x$
$x < 0$	${a^x} > 1$
$x = 0$	${a^0} = 1$
$0 < x < 1$	$0 < {a^x} < 1$
$x = 0$	${a^x} = 1$
$x > 1$	$0 < {a^x} < a < 1$

Når $a < 1$, er funktionen $f\left( x \right) = {a^x}$ en strengt faldende funktion, det vil sige, hvis \({x_2} > {x_1}\ ), så:

${a^{{x_2}}} < a_{}^{{x_1}}$ $f\left( {{x_2}} \right) < f\left( {{x_1}} \right) $ Når et fænomen er modeller med en eksponentiel funktion, med $a < 1$, siger vi, at den præsenterer et henfald eller fald eksponentiel. Den følgende graf illustrerer adfærden af ${a^x}$, i dets tre forskellige tilfælde.

Anvendelser af den eksponentielle funktion

Eksempel 1 Befolkningstilvækst

Vi vil betegne med ${P_0}$ den oprindelige befolkning og med $r \ge 0$ befolkningstilvæksten, hvis befolkningsraten forbliver konstant over tid; funktionen

$P\left( t \right) = {P_0}{\left( {1 + r} \right)^t};$

Find bestanden på tidspunktet t.

Praktisk eksempel 1

Befolkningen i Mexico er i år 2021 126 millioner og præsenterede en årlig vækst på 1,1%, Hvis denne vækst opretholdes, hvilken befolkning vil der være i Mexico i år 2031, i år 2021?

Løsning

I dette tilfælde ${P_o} = 126$ og $r = \frac{{1.1}}{{100}} = 0,011$, så skal du bruge:

$P\left( t \right) = {P_0}{\left( {1 + .0011} \right)^t}$

Følgende tabel viser resultaterne

År	forløbet tid ($t$)	Beregning	Befolkning (millioner)
2021	0	$P\left( t \right) = 126{\left( {1.0011} \right)^0}$	126
2031	10	$P\left( t \right) = 126{\left( {1.0011} \right)^{10}}$	140.57
2051	30	$P\left( t \right) = 126{\left( {1.0011} \right)^{30}}$	174.95

Eksempel 2 Beregning af renters rente

Banker tilbyder en årlig rente, men den reelle rente afhænger af, hvor mange måneder du investerer den; Hvis du f.eks. tilbydes en årlig rente på r%, er den reelle månedlige rente $\frac{r}{{12}}$%, den tomånedlige rente er $\frac{r}{6}$%, kvartalsvis er $\frac{r}{4}$%, kvartalsvis er $\frac{r}{3}$%, og semesteret er $\frac{r}{2}$%.

Praktisk eksempel 2

Antag, at du investerer 10.000 i en bank, og de tilbyder dig følgende årlige rentesatser:

Tidsindskud	Årlig sats	perioder på et år	faktiske sats	Akkumulerede penge i $k$ måneder
to måneder	0.55%	6	$\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}$	$10000{\left( {1 + 0,00091667} \right)^{\frac{k}{2}}}$
tre måneder	1.87%	4	$\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}$	$10000{\left( {1 + 0,00461667} \right)^{\frac{k}{3}}}$
seks måneder	1.56%	2	$\frac{{1,56\% }}{4} = 0,78{\rm{\% }}$	$10000{\left( {1 + 0,0078} \right)^{\frac{k}{6}}}$

Tallet $e$, Eulers konstante og vedvarende interesse.

Antag nu, at vi har en startkapital $C$, og vi investerer den til en fast rente $r > 0$, og vi deler året op i $n$ perioder; den akkumulerede kapital i et år er lig med:

$A = \;C{\venstre( {1 + \frac{r}{n}} \right)^n}$

For at analysere, hvordan den akkumulerede kapital opfører sig, når $n$, vokser, vil vi omskrive den akkumulerede kapital på et år:

$A = \;C{\venstre( {1 + \frac{r}{n}} \right)^n}$$A = \;C{\venstre( {1 + \frac{1} {{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right) r}},$

ved at gøre $m = \frac{n}{r}$, får vi:

$A = C{\venstre( {1 + \frac{1}{m}} \right)^{mr}}$$A = C{\venstre( {{{\venstre( {1 + \ frac{1}{m}} \right)}^m}} \right)^r}.$

Når $n$ vokser, vokser $m = \frac{n}{r} også.$

Efterhånden som $m = \frac{n}{r},$ vokser, nærmer udtrykket ${\left( {1 + \frac{1}{m}} \right)^m}$ det, der kaldes Euler konstant eller tal:

$e \ca. 2,718281828 \ldots .$

Eulers konstant har ikke et endeligt eller periodisk decimaludtryk.

Vi har følgende tilnærmelser

$C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \ca. C{e^r},$ $C{\venstre( {1 + \frac{r}{n}} \right)^{ns}} \ca. C{e^{rs}}.$

Til udtrykket:

$A = \;C{e^r},$

Vi kan fortolke det på to måder:

1.- Som det maksimale beløb, vi kan akkumulere på et år, når vi investerer kapital $C,\;$ med en årlig kurs $r.$

2.- Som det beløb, vi ville akkumulere på et år, hvis vores kapital løbende blev geninvesteret til en årlig kurs $r.$

$T\venstre( s \højre) = \;C{e^{rs}},$

er det akkumulerede beløb, hvis $s$ år investeres med løbende rente.

Konkret eksempel 3

Nu vender vi tilbage til en del af konkret eksempel 2, hvor den årlige sats er 0,55 % i to-månedlige rater. Beregn den kapital, der akkumuleres, hvis startkapitalen er 10.000 og geninvesterer et halvt år, to år, 28 måneder.

$10{\left( {1.00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525$

som tabellen nedenfor viser, er værdien af $m = \frac{n}{r},$ ikke "lille", og tabellen ovenfor angiver, at ${\left( {1 + \frac{1}{ m}} \right)^m}$ er tæt på Eulers konstant.

Tid	Antal perioder ($k$)	Akkumuleret kapital, i tusinder, geninvesteret hver anden måned
Halvt år	3	$10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525$
To år	12	$10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557$
38 måneder	19	$10{\venstre( {1.00091667} \right)^{19}} = 10.\;175612$

Tid	Tid af år ($s$)	Akkumuleret kapital, i tusindvis, investerer med løbende rente
Halvt år	$s = \frac{1}{2}$	$10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538$
To år	$s = 2$	$10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607$
38 måneder	$s = \frac{{19}}{6}$	$10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692$

Eksempel 2 Afskrivninger

Praktisk eksempel 1

En computer afskriver 30% hvert år, hvis en computer koster $20.000 pesos, skal du bestemme prisen på computeren i $t = 1,12,\;14,\;38$ måneder.

I dette tilfælde har man:

$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0,30} \right)^t}$

Med $t$ i år, giver substituering af $t$ i følgende tabel

tid i måneder	tid i år	beregninger	Numerisk værdi
1	$\frac{1}{{12}}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}$	19414.289
12	1	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}$	14000
14	$\frac{7}{6}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}$	13192.012
38	$\frac{{19}}{6}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}$	6464.0859

Tags sky

Bedømmelse

Visninger

Kommentarer

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\)	\({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\left( {ab} \right)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) for hver \(a \ne 0\)

Værdien af \(x\)
\(x < 0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x} < a\)
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(a < {a^x}\)

Værdien af \(x\)
\(x < 0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x} < a < 1\)

Tid	Tid af år (\(s\))	Akkumuleret kapital, i tusindvis, investerer med løbende rente
Halvt år	\(s = \frac{1}{2}\)	\(10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\)
To år	\(s = 2\)	\(10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607\)
38 måneder	\(s = \frac{{19}}{6}\)	\(10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

År	forløbet tid (\(t\))	Beregning	Befolkning (millioner)
2021	0	\(P\left( t \right) = 126{\left( {1.0011} \right)^0}\)	126
2031	10	\(P\left( t \right) = 126{\left( {1.0011} \right)^{10}}\)	140.57
2051	30	\(P\left( t \right) = 126{\left( {1.0011} \right)^{30}}\)	174.95

Tidsindskud	Årlig sats	perioder på et år	faktiske sats	Akkumulerede penge i \(k\) måneder
to måneder	0.55%	6	\(\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}\)	\(10000{\left( {1 + 0,00091667} \right)^{\frac{k}{2}}}\)
tre måneder	1.87%	4	\(\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}\)	\(10000{\left( {1 + 0,00461667} \right)^{\frac{k}{3}}}\)
seks måneder	1.56%	2	\(\frac{{1,56\% }}{4} = 0,78{\rm{\% }}\)	\(10000{\left( {1 + 0,0078} \right)^{\frac{k}{6}}}\)

Tid	Antal perioder (\(k\))	Akkumuleret kapital, i tusinder, geninvesteret hver anden måned
Halvt år	3	\(10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525\)
To år	12	\(10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 måneder	19	\(10{\venstre( {1.00091667} \right)^{19}} = 10.\;175612\)

tid i måneder	tid i år	beregninger	Numerisk værdi
1	\(\frac{1}{{12}}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	6464.0859