Definition der Exponentialfunktion

Die Exponentialfunktion modelliert verschiedene natürliche Phänomene sowie soziale und wirtschaftliche Situationen, weshalb es wichtig ist, Exponentialfunktionen in verschiedenen Kontexten zu identifizieren.

Erinnern wir uns, dass für eine Zahl \({a^1} = a,{a^2} = aa,\;{a^3} = aaa\) definiert ist, im Allgemeinen haben wir das für jede \(n\ ) natürliche Zahl:

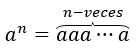
Im Fall \(a \ne 0\) haben wir das: \({a^0} = 1,\;\) in der Tat, wenn \(a \ne 0,\) es sinnvoll ist, die Operation \ (\frac{a}{a} = 1;\) bei Anwendung des Exponentengesetzes gilt:

\(\frac{a}{a}=1\)

\({a^{1 – 1}} = 1\)

\({a^0} = 1.\)

Wenn \(a = 0\) ist, macht die vorherige Argumentation keinen Sinn, daher fehlt dem Ausdruck \({0^0},\) eine mathematische Interpretation.

Für den Fall, dass \(b > 0\) und \({b^n} = a,\) wahr ist, sagt man, dass \(b\) die n-te Wurzel von \(a\) ist und normalerweise ist bezeichnet als \ (b = {a^{\frac{1}{n}}},\;\) oder \(b = \sqrt[n]{a}\).

Wenn \(a < 0\), gibt es keine reelle Zahl \(b\), so dass \({b^2} = a;\) weil \({b^2} \ge 0;\;\ ) so ist Ausdrücke der Form \({a^{\frac{m}{n}}}\), wird für \(a < 0.\) nicht berücksichtigt. Im folgenden algebraischen Ausdruck: \({a^n}\) \(a \ ) heißt Basis, und \(n\) ist es Exponent genannt, wird \({a^n}\) die Potenz\(\;n\) von \(a\) oder auch \(a\) hoch \(n,\;\)se genannt die folgenden Gesetze einhalten der Exponenten:

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\)	\({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\links({ab} \rechts)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) für jedes \(a \ne 0\)

Die Exponentialfunktion hat die Form:

\(f\links( x \rechts) = {a^x}\)

wobei \(a > 0\) eine Konstante und die unabhängige Variable der Exponent \(x\) ist.

Um eine Analyse der Exponentialfunktion durchzuführen, betrachten wir drei Fälle

Fall 1 Wenn die Basis \(a = 1.\)

In diesem Fall ist \(a = 1,\) die Funktion \(f\left( x \right) = {a^x}\) eine konstante Funktion.

Fall 2 Wenn die Basis \(a > 1\)

In diesem Fall haben wir Folgendes:

Wert von \(x\)
\(x < 0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x} < a\)
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(a < {a^x}\)

Die Funktion \(f\left( x \right) = {a^x}\) ist eine streng steigende Funktion, d. h. wenn \({x_2} > {x_1}\), dann gilt:

\({a^{{x_2}}} > a_{}^{{x_2}}\)

\(f\left( {{x_2}} \right) > f\left( {{x_1}} \right)\)

Wenn ein Phänomen mit einer Exponentialfunktion modelliert wird, mit \(a > 1\), sagen wir, dass es ein exponentielles Wachstum darstellt.

Fall 2 Wenn die Basis \(a < 1\).

Wert von \(x\)
\(x < 0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x} < a < 1\)

Wenn \(a < 1\), ist die Funktion \(f\left( x \right) = {a^x}\) eine streng fallende Funktion, d. h. wenn \({x_2} > {x_1}\ ), So:

\({a^{{x_2}}} < a_{}^{{x_1}}\) \(f\left( {{x_2}} \right) < f\left( {{x_1}} \right) \) Wenn ein Phänomen ist Modelle mit einer Exponentialfunktion, mit \(a < 1\), sagen wir, dass es einen Abfall oder eine Abnahme darstellt exponentiell. Das folgende Diagramm veranschaulicht das Verhalten von \({a^x}\) in seinen drei verschiedenen Fällen.

Anwendungen der Exponentialfunktion

Beispiel 1 Bevölkerungswachstum

Wir bezeichnen mit \({P_0}\) die Anfangsbevölkerung und mit \(r \ge 0\) die Bevölkerungswachstumsrate, wenn die Bevölkerungsrate über die Zeit konstant bleibt; die Funktion

\(P\left( t \right) = {P_0}{\left( {1 + r} \right)^t};\)

Finden Sie die Population zum Zeitpunkt t.

Praxisbeispiel 1

Die Bevölkerung Mexikos beträgt im Jahr 2021 126 Millionen und weist ein jährliches Wachstum von 1,1 % auf, Wenn dieses Wachstum anhält, wie viele Einwohner wird es im Jahr 2031 in Mexiko geben? 2021?

Lösung

In diesem Fall \({P_o} = 126\) und \(r = \frac{{1.1}}{{100}} = 0.011\), also sollten Sie verwenden:

\(P\left( t \right) = {P_0}{\left( {1 + .0011} \right)^t}\)

Die folgende Tabelle zeigt die Ergebnisse

Jahr	verstrichene Zeit (\(T\))	Berechnung	Bevölkerung (Millionen)
2021	0	\(P\left( t \right) = 126{\left( {1.0011} \right)^0}\)	126
2031	10	\(P\left( t \right) = 126{\left( {1.0011} \right)^{10}}\)	140.57
2051	30	\(P\left( t \right) = 126{\left( {1.0011} \right)^{30}}\)	174.95

Beispiel 2 Zinseszinsberechnung

Banken bieten einen jährlichen Zinssatz an, aber der reale Zinssatz hängt davon ab, wie viele Monate Sie ihn investieren; Wenn Ihnen beispielsweise ein jährlicher Zinssatz von r% angeboten wird, beträgt der tatsächliche monatliche Zinssatz \(\frac{r}{{12}}\)%, der zweimonatliche Zinssatz jedoch \(\frac{r}{6}\)%, vierteljährlich ist \(\frac{r}{4}\)%, vierteljährlich ist \(\frac{r}{3}\)% und das Semester ist \(\frac{r}{2}\)%.

Praxisbeispiel 2

Angenommen, Sie investieren 10.000 in eine Bank und sie bietet Ihnen die folgenden jährlichen Zinssätze:

Festgelder	Jährliche Rate	Perioden in einem Jahr	tatsächlicher Kurs	Angesammeltes Geld in \(k\) Monaten
zwei Monate	0.55%	6	\(\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}\)	\(10000{\left( {1 + 0.00091667} \right)^{\frac{k}{2}}}\)
drei Monate	1.87%	4	\(\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}\)	\(10000{\left( {1 + 0.00461667} \right)^{\frac{k}{3}}}\)
sechs Monate	1.56%	2	\(\frac{{1,56\% }}{4} = 0,78{\rm{\% }}\)	\(10000{\left( {1 + 0.0078} \right)^{\frac{k}{6}}}\)

Die Zahl \(e\), Eulers konstantes und kontinuierliches Interesse.

Nehmen wir nun an, wir haben ein Anfangskapital \(C\) und investieren es zu einem festen Zinssatz \(r > 0\), und wir teilen das Jahr in \(n\) Perioden; Das in einem Jahr angesammelte Kapital ist gleich:

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)

Um zu analysieren, wie sich das akkumulierte Kapital verhält, wenn \(n\), wächst, schreiben wir das akkumulierte Kapital in einem Jahr um:

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)\(A = \;C{\left( {1 + \frac{1} {{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right) r}},\)

mit \(m = \frac{n}{r}\) erhalten wir:

\(A = C{\left( {1 + \frac{1}{m}} \right)^{mr}}\)\(A = C{\left( {{{\left( {1 + \ frac{1}{m}} \right)}^m}} \right)^r}.\)

Wenn \(n\) wächst, wächst auch \(m = \frac{n}{r}.\)

Wenn \(m = \frac{n}{r},\) wächst, nähert sich der Ausdruck \({\left( {1 + \frac{1}{m}} \right)^m}\) dem, was man den nennt Euler-Konstante oder Zahl:

\(e \approx 2.718281828 \ldots .\)

Die Eulersche Konstante hat keinen endlichen oder periodischen Dezimalausdruck.

Wir haben die folgenden Näherungen

\(C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \approx C{e^r},\) \(C{\left( {1 + \frac{r}{n}} \right)^{ns}} \approx C{e^{rs}}.\)

Zum Ausdruck:

\(A = \;C{e^r},\)

Wir können es auf zwei Arten interpretieren:

1.- Als maximaler Betrag, den wir in einem Jahr ansammeln können, wenn wir Kapital \(C,\;\) zu einer jährlichen Rate \(r.\) anlegen

2.- Als der Betrag, den wir in einem Jahr ansammeln würden, wenn unser Kapital kontinuierlich zu einer jährlichen Rate reinvestiert würde \(r.\)

\(T\left( s \right) = \;C{e^{rs}},\)

ist der angesammelte Betrag, wenn \(s\) Jahre mit fortlaufender Verzinsung investiert werden.

Konkretes Beispiel 3

Nun kehren wir zu einem Teil des konkreten Beispiels 2 zurück, wo die jährliche Rate 0,55 % in zweimonatlichen Raten beträgt. Berechnen Sie das Kapital, das sich ansammelt, wenn das Anfangskapital 10.000 beträgt und ein halbes Jahr, zwei Jahre, 28 Monate reinvestiert wird.

\(10{\left( {1.00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525\)

Wie die folgende Tabelle zeigt, ist der Wert von \(m = \frac{n}{r},\) nicht „klein“, und die obige Tabelle zeigt, dass \({\left( {1 + \frac{1}{ m}} \right)^m}\) liegt nahe an der Eulerschen Konstante.

Zeit	Anzahl der Perioden (\(k\))	Angesammeltes Kapital in Tausend, das alle zwei Monate reinvestiert wird
Halbes Jahr	3	\(10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525\)
2 Jahre	12	\(10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 Monate	19	\(10{\left( {1.00091667} \right)^{19}} = 10.\;175612\)

Zeit	Jahreszeit (\(s\))	Angesammeltes Kapital in Tausenden wird mit fortlaufender Verzinsung investiert
Halbes Jahr	\(s = \frac{1}{2}\)	\(10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\)
2 Jahre	\(s = 2\)	\(10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607\)
38 Monate	\(s = \frac{{19}}{6}\)	\(10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

Beispiel 2 Abschreibung

Praxisbeispiel 1

Ein Computer verliert jedes Jahr 30 % an Wert, wenn ein Computer 20.000 Pesos kostet, bestimmen Sie den Preis des Computers für \(t = 1,12,\;14,\;38\) Monate.

In diesem Fall hat man:

\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0,30} \right)^t}\)

Mit \(t\) in Jahren ergibt das Ersetzen von \(t\) in der folgenden Tabelle

Zeit in Monaten	Zeit in Jahren	Berechnungen	Numerischer Wert
1	\(\frac{1}{{12}}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	6464.0859