Coulomb's Law Example

Coulum's law was first produced by the creation of the balance of Coulum which was created by the French scientist Charles Augustin Coulomb, he invented a balance to study the twist of fibers and wires, later this same balance used it then to reproduce in a small space, the laws of attraction and static charge that Isaac Newton and Johannes Kepler enunciated on the relationship of the forces of gravity between the planets

The torsion balance consists of two glass cylinders, one long and thin, at the end of which a silver rod is suspended. On the other side of the rod that is on a wider cylinder and with a numerical scale, there is another horizontal rod, at the end of which he placed a ball of elder marrow. At the top of the scale, there is a hole through which another sphere of elderberry pith attached to a rod is inserted.

When both rods are brought together without static charges, there are no forces of attraction or repulsion, and they remain at rest. When a charge is applied to them by an electrode, they will reject each other if they are of equal signs, or they will move closer if they are of opposite signs.

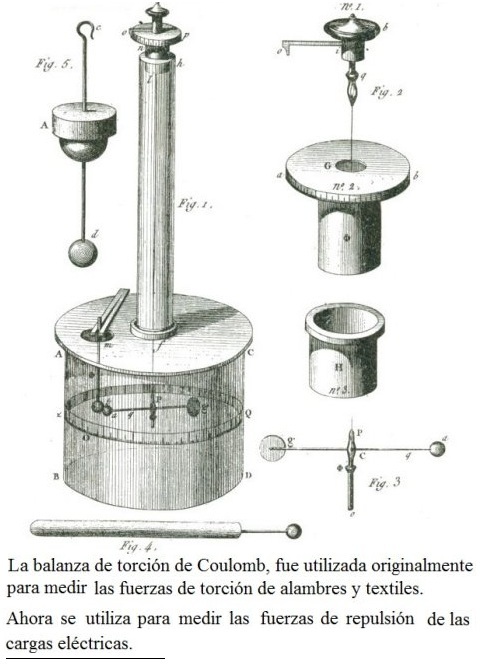
This experiment was then carried out on spheres suspended in vacuum. These experiments led him to express the law of electrostatic charges, better known as Coulomb law, which says: “The force that two electric charges exert on each other is directly proportional to the product of their electrostatic charges and inversely proportional to the square of the distance that the To stop."

This means that two electrostatic charges will repel each other with a certain force, which is initially calculated by the product of charge 1 and charge 2 (q₁ Because₂). And this repulsion force will vary directly as a function of the increase or decrease of both or one of the charges, considering that the distance between the charged spheres is constant.

When the distance varies, the force will vary in inverse proportion to the square of the distance, that is, if, for example, the charges remain equal and the initial distance is doubled, then we will have 2 X 2 = 4 and its inverse relationship indicates that the force will be ¼ of the force with distance 1.

This is explained with the following formulas:

F = q₁* what₂ for a constant distance.
F = q₁* what₂/ d² for a variable distance.

In addition, it is necessary to apply a constant (k), which will allow us to determine the force that always acts in relation to the load. This constant is determined by the repulsive force, the distance, the charge, and the medium that divides the charges, which it can have different degrees of conductivity due to its conductivity and density, which is called the coefficient dielectric.

MEASUREMENT UNITS. As in all calculations of physical quantities, we use various units of measurement. For these calculations, the units are as follows:

F: Newton (1 newton is equal to the force needed to move 1 kilogram through 1 meter every second)

Charge (q1, q2): Coulumb (1 Coulomb equals 6.28 X 10¹⁸ electrons)
Distance (d): Meter (Unit of measure in the metric system)

K: The dielectric constant is determined by the electrostatic rejection force in two charges of the same magnitude, which in vacuum is 8.988 X 10⁹ Newton, for every meter squared and divided by the square of the load. For practical purposes, the value is rounded to 9 X 10⁹ Nm²/ q². Then we will have the following formulas:

F = (k) q₁ Because₂ For fixed distances.
F = (k) q₁ Because₂ / d² for variable distances.

If we develop this last formula, we will have:

F = (9X10⁹ m² / q²) Because₁ Because₂ / d²

This formula is valid for the Void. In the case that the charges are in a different medium, then the constant will be divided by the dielectric coefficient of the medium. The formulas will then be as follows:

F = (k / e) q₁ Because₂ For fixed distances.
F = (k / e) q₁ Because₂ / d² for variable distances.

Dielectric constant of some substances:

Empty: 1
Air: 1
Wax: 1.8
Water: 80
Alcohol: 15
Paper: 1.5
Paraffin: 2.1

4 examples of Coulomb's Law:

Example 1.

Calculate the force with which two spheres with charges of 3 X 10 repel^-5 Coulomb and 5 X 10^-5, at a distance of 40 centimeters, in a vacuum.

F =?
what₁ = 1 X 10^-5
what₂ = 1 X 10^-5
d = .4 meters
k = 9 X 10⁹ m²/ d²
what₁ Because₂ = (3 X 10^-3) (5 X 10^-5) = 1 X 10^-10
d² = 0.16 m
what₁ Because₂ / d^{2 =}1 X 10^-8/0.16 = 6.25 X 10^-10
k x (q₁ Because₂ / d²) = (9 X 10⁹) (6.25/10-¹⁰) = 5,625 N.

Example 2

Calculate with the same data of the previous example, the force with which the charges are repelled per hour with equal charges of 2.5 X 10^-6 Coulomb.

F =?
what₁ = 2.5 X 10^-6
what₂ = 2.5 X 10^-6
d = .4 meters
k = 9 X 10⁹ m²/ d²
what₁ Because₂ = (2.5 X 10^-6) (2.5 X 10^-6) = 6.25 X 10^-12
d² = 0.16 m
what₁ Because₂ / d^{2 =}15 X 10^-8/0.16 = 39.0625 X 10^-12
k x (q₁ Because₂ / d²) = (9 X 10⁹) (39.0625 X 10^-12) = 0.315 N. (31.5 X 10^-2 N)

Example 3

Using the same data as in example 2, calculate the repulsion force at twice the distance, that is, at 80 centimeters.

F =?
what₁ = 2.5 X 10^-6
what₂ = 2.5 X 10^-6
d = .8 meters
k = 9 X 10⁹ m²/ d²
what₁ Because₂ = (2.5 X 10^-6) (2.5 X 10^-6) = 6.25 X 10^-12
d² = 0.64 m
what₁ Because₂ / d^{2 =}15 X 10^-8/0.16 = 9.765625 X 10^-12
k x (q₁ Because₂ / d²) = (9 X 10⁹) (9.765625 X 10^-12) = 0.0878 N. (8.78 X10^-2 N)

Example 4

Calculate example 3, in a different dielectric medium, now in alcohol.

F =?
what₁ = 2.5 X 10^-6
what₂ = 2.5 X 10^-6
d = .8 meters
k = 9 X 10⁹ m²/ d²
e = 15
what₁ Because₂ = (2.5 X 10^-6) (2.5 X 10^-6) = 6.25 X 10^-12
d² = 0.64 m
what₁ Because₂ / d^{2 =}15 X 10^-8/0.16 = 9.765625 X 10^-12
k / e = (9 X 10⁹) / 15 = 6 X 10⁸
k X (q₁ Because₂ / d²) = (6 X 10⁸) (9.765625 X 10^-12) = 0.00586 N (5.86 X 10^-3 N)