Characteristics Of A Vector

A vector is the graphical representation of a physical quantity called a vector quantity, inscribed within a Cartesian plane format. Vector quantities have three components: quantity, direction, and sense. Some of these magnitudes are the displacement (travel or distance), the speed and the force. With vectors, the interaction of two or more vector quantities is also represented, to obtain and represent the final result of that interaction.

Vectors are used in different fields, such as engineering, theoretical and practical physics, architecture, in measurements astronomical or in the design of devices, as well as in mathematics, being key in topics such as vector algebra and kinematics.

Main characteristics of a vector:

Magnitude. The magnitude is the measurable physical phenomenon that is represented by the vector.

Quantity. Quantity, also known as intensity or modulus, is the units of measurement represented by the length of the vector from the point of origin to the tip.

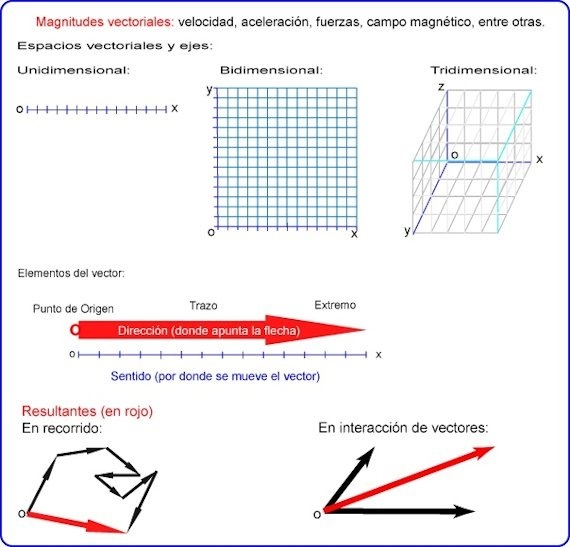
Vectorial space. Also called Euclidean space, it is the type of Cartesian plane on which the vector is drawn and in which its direction is indicated. It can be one-dimensional (X axis, number line), two-dimensional (XY axes, Cartesian coordinates) and three-dimensional (XYZ axes, spatial trace).

Direction. The direction is the characteristic of the vector that indicates the plane on which the magnitude is acting. It can be in any of the three-dimensional Euclidean planes (XYZ Axes). When it comes to quantities that act in the same direction, they are generally represented on the horizontal axis of the Cartesian plane. (X axis), usually represented as a segment of a number line, and on which each of the vectors.

Sense. As in the number line, the direction is determined from the point of origin indicating in which direction the magnitude in question is being applied. When it acts in only one direction, (X axis) the sense is expressed in a positive or negative sense. When it acts in two planes (X and Y axes), its sense can be expressed in the form of coordinates of a Cartesian plane (XY), or either, as movements in a cardinal point coordinate system (north, south, northeast), or a combination of both of them. In the case of three-dimensional vectors, the direction is indicated from the point of origin to the point of arrival, with a spatial coordinate representation (XYZ).

Point of origin and end. The point of origin, also called the application point or simply the origin, is the point from which the vector is drawn, usually marked with a point or a small circle. The endpoint is the end of the vector stroke, and is represented by an arrowhead.

Stroke. A vector is always represented as a line segment, originating at the point of application and ending at the endpoint.

Resulting. The resultant is the vector that is drawn from the point of origin of a vector to the end of the last vector drawn, when each segment represents the continuity of a magnitude (as happens in the representation of a mobile that changes direction several times. In these cases, vectors can be added that go in one direction or the other, and the result will be the distance total traveled, which is the vector that is drawn from the point of origin to the end of the last stroke). The vector that represents the final magnitude obtained when two vectors interact with different directions and senses, and with the same point of application or point originally. (This happens when, for example, we tie two threads at the same point on an object placed on the corner of a table and then begin to pull each thread to a different corner of the table; the result will be that the object will move diagonally across the table; this diagonal movement will vary in relation to the force applied to each of the threads. The line of this diagonal movement will be the result).