Definition of Quantum Numbers

Candela Rocío Barbisan | Dec. 2021
Chemical engineer

Quantum numbers are a set of numbers represented by letters that, depending on the position of the electron to which they are referred, take different values within a possible range. Now we are going to describe each of them and we will see examples of how they are applied according to the electron we want to designate.

Principal quantum number ("n")

It is closely related to Energy that the electron possesses. The higher “n”, the higher the energy, since this number is related to the size of the orbital. Mathematically, it tells us the period where the electron is located, and as we know from the electronic configurations of the elements of the Periodic table, there are physically up to seven levels of energy. Therefore, "n" can vary from one to seven depending on the distance to which the electron of the atom is located.

Secondary or azimuthal quantum number ("ℓ")

This number allows identify the energy sublevel that the electron is occupying, so, again, the higher the azimuthal quantum number, the higher the energy the electron has. Mathematically, "ℓ" will represent the sublevels "s", "p", "d" and "f" that we identify electron configurations of the elements of the Periodic Table. That is why it can take values ​​ranging from zero up to ("n" -1) where "n" is the principal quantum number.

For example, if n = 1, then ℓ can only be zero, since it corresponds to the energy sublevel "s". Whereas, if n = 2, ℓ can value both zero and one, since we can be referring to an electron of the sublevel "s" or the sublevel "p" respectively. In this way we identify: ℓ = 0 for energy sublevel “s”, ℓ = 1 for energy sublevel “p”, ℓ = 2 for energy sublevel “d” and ℓ = 3 for energy sublevel “f”.

It should be noted that, according to "n", the energy sublevels "s", "p", "d" and "f" can add orbitals and, therefore, contain more electrons. For example, at n = 1, ℓ = 0 with a single "s" sublevel and a single orbital that can contain two electrons. For n = 2, ℓ = 0 with a sublevel “s” or ℓ = 1 with a sublevel “p” that can contain three orbitals and accommodate six electrons.

For n = 3, ℓ = 0 with a sublevel “s” or ℓ = 1 with a sublevel “p” that can contain three orbitals and accommodate six electrons or ℓ = 2 with the sublevel "d" that can contain five orbitals and accommodate ten electrons.

Finally, for n = 4, ℓ = 0 with a sublevel “s” or ℓ = 1 with the sublevel “p” that can contain three orbitals and accommodate six electrons or ℓ = 2 with the sublevel “d” that can contain five orbitals and house ten electrons or ℓ = 3 with sublevel “f” that can contain seven orbitals and house fourteen electrons.

If we wanted to represent these orbitals in space, their shape would be something like the following:

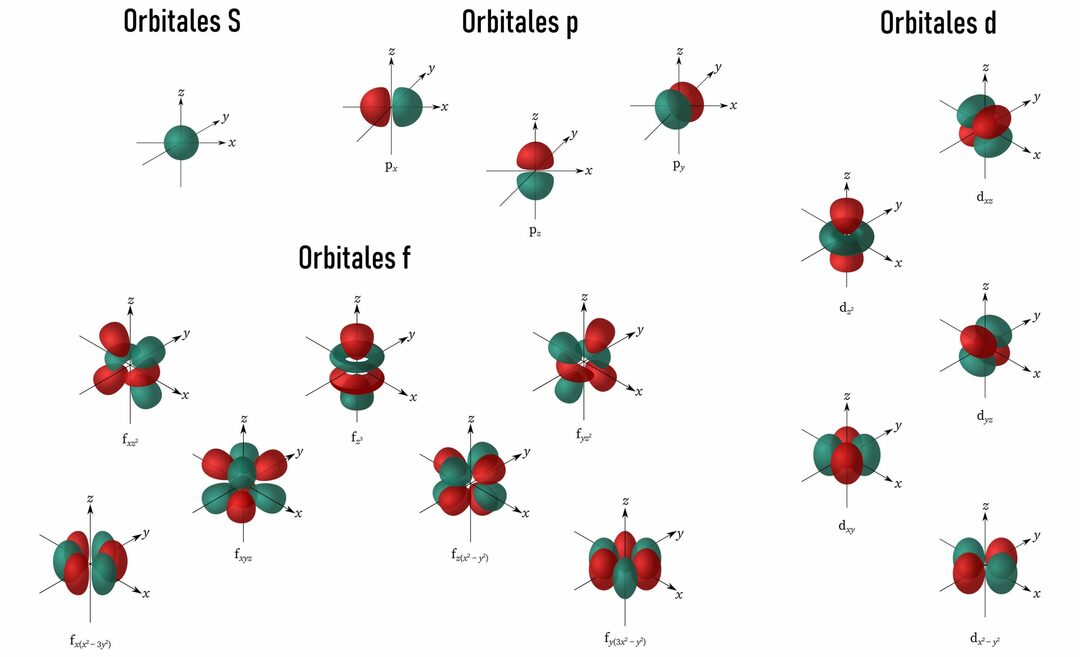
Img: ChemistryGod

Magnetic quantum number ("m")

It is related to the orientation of the orbital in space and is related to the number of orbitals that each sublevel has. Therefore, the value it takes ranges from "-ℓ" to "ℓ". For example, for ℓ = 1, sublevel “p” contains up to 3 orbitals, so “m” acquires values ​​such as -1, 0 or 1. Similarly, for ℓ = 2 sublevel "d" contains up to 5 orbitals, so "m" can be: -2, -1, 0, 1 or 2. Similarly, it is completed for ℓ = 0 or ℓ = 4.

Spin quantum number ("s")

Related to the magnetic properties of the electron and they serve to identify the direction of rotation of the electrons that are located within the same orbital, since each of them will have a different sign. Therefore, "s" can take the value of +1/2 or -1/2.

Let's take Chlorine as an example, to identify quantum numbers in its electrons housed in the last energy level. For this we need to know its electronic configuration, which is: 1s² 2s² 2 P⁶3s²3p⁵. The electrons of the last level are those housed in level 3, so: n = 3. Then, ℓ = 0 or ℓ = 1, for electrons housed in sublevels "s" or "p" respectively.

Now, for ℓ = 0 (3s²), m = 0 and s is worth +1/2 and -1/2 respectively in each of the electrons housed there. For ℓ = 1 (3p⁵), m = -1,0,1, while s is worth +1/2 and -1/2 respectively in each of the electrons housed there for m = -1 and 0, while the Orbital designated as m = 1 is not complete with two electrons, so we must choose s = +1/2 or -1/2, whichever is chosen by convention.