Arrhenius Equation Definition

This equation is a modification of the Van't Hoff equation and is based on empirical data, that is, experiences carried out and studied to find the correlation that best fits. Their expression is summarized to:

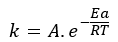
Where, k is the kinetic constant of the reaction, A is the frequency factor (a constant involving the frequency of collisions), Ea is the Energy of activation (J/ mol) required to carry out the reaction, that is, the minimum energy necessary for there are effective collisions between molecules, R (J/ K.mol) is the universal gas constant and T is the actual the temperature of reaction.

It should be noted that the value of k, unique for a given temperature, can be obtained from the Law of reaction speed further:

being v the

speed of reaction, for a reaction of type: A + B → C. Where n and m are the reaction orders with respect to A and B.

Experimentally, it is observed that the speed of a chemical reaction increases with increasing temperature. Meanwhile, the reaction rate constant will increase with increasing temperature and decreasing activation energy. However, we note that the dependence between the reaction rate constant and temperature is exponential, however, many times we will see the equation modified to its logarithmic form, so linearized:

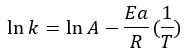
This model allows us to find a linear regression where the ordinate axis is represented by ln (k) while on the abscissa (1/T), having ln (A) as ordinate to the origin and ln (A) as slope -Ea/R.

Applicability

First and most common use is the determination of the rate constant of the chemical reaction and, From this value, it is also possible (by Speed ​​Law) to determine the speed of reaction. Meanwhile, the Arrhenius Equation is also useful to know the Activation Energy and observe the dependence between both values.

For example, if values ​​of reaction rate constants were determined for different temperatures, from the slope of the curve ln (k) vs. (1/T) it is possible to obtain the activation energy value of the reaction.

*Illustration of work "Research Applied to Mineral Processing and Hydrometallurgy", published in 2015, by the UAdeC

Here you can see the linearization raised above.

The value of the Activation Energy gives us an idea of ​​how the speed responds with respect to changes in temperature, that is, a High Activation Energy corresponds to a reaction rate that is very sensitive to temperature (with a steep slope), whereas, a small Activation Energy corresponds to a reaction rate that is relatively insensitive to variations in the temperature.

On the other hand, if the Activation Energy and the value of the reaction rate constant at a given temperature, the model allows predicting the reaction rate at another given temperature, since for two conditions different you have:

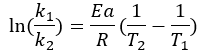
In other fields, such as materials engineering and foods, this Equation has been developed and implemented in models that allow properties and behaviors to be predicted from changes in reaction temperatures.

Likewise, this Equation is used in the field of electronics for the study of metal hydride batteries and their service life. In addition, this Equation was developed to obtain diffusive coefficients, creep rates and other thermal modeling.

Limitations

The most widespread limitation of this Equation is its applicability only in aqueous solutions. Although it was modified to be applied to solids, in principle, it was proposed for solutions whose solvent is water.

Likewise, it should be noted that it is an empirical model and not exact, based on multiple experiences and statistical results.