What are Maxwell's Equations, and how are they defined?

Angel Zamora Ramirez | Jul. 2022
Degree in physics

Before these equations, it was said that the electric and magnetic forces were "forces at a distance", no physical means was known by means of which this type of interaction would occur. After many years of research on electricity Y magnetism, Michael Faraday intuited that there would have to be something physical in the space between the charges and the electric currents that would allow them to interact with each other and manifest all the electrical and magnetic phenomena that were known, he at first referred to this as "lines of force", which led to the idea of ​​the existence of an electromagnetic field.

Building on Faraday's idea, James Clerk Maxwell develops a field theory represented by four partial differential equations. Maxwell referred to this as "electromagnetic theory" and was the first to incorporate this type of mathematical language into a physical theory. Maxwell's equations in their differential form for vacuum (that is, in the absence of dielectric and/or polarizable materials) are as follows:

\(\nabla \cdot \vec{E}=\frac{\rho }{{{\epsilon }_{0}}}\)
\(\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\)
\(\nabla \cdot \vec{B}=0\)
\(\nabla \times \vec{B}={{\mu }_{0}}\vec{J}+{{\mu }_{0}}{{\epsilon }_{0}}\frac {\partial \vec{E}}{\partial t}\)
Maxwell's equations for the vacuum in its differential form

Where \(\vec{E}~\)is the electric field, \(\vec{B}~\)is the magnetic field, \(\rho ~\)is the density of electric charge, \(\vec{J}~~\)is a vector associated to a electric current, \({{\epsilon }_{0}}~\)is the electrical permittivity of a vacuum and \({{\mu }_{0}}~~\)is the magnetic permeability of a vacuum. Each of these equations corresponds to a law of electromagnetism and has a meaning. I will briefly explain each of them below.

Gauss's law

\(\nabla \cdot \vec{E}=\frac{\rho }{{{\epsilon }_{0}}}\)
Gauss's law for the electric field

What this first equation tells us is that the electric charges are the sources of the electric field, this electric field “diverges” directly from the charges. Also, the direction of the electric field is dictated by the sign of the electric charge producing it, and how close the field lines are indicates the magnitude of the field itself. The image below somewhat summarizes what has just been mentioned.

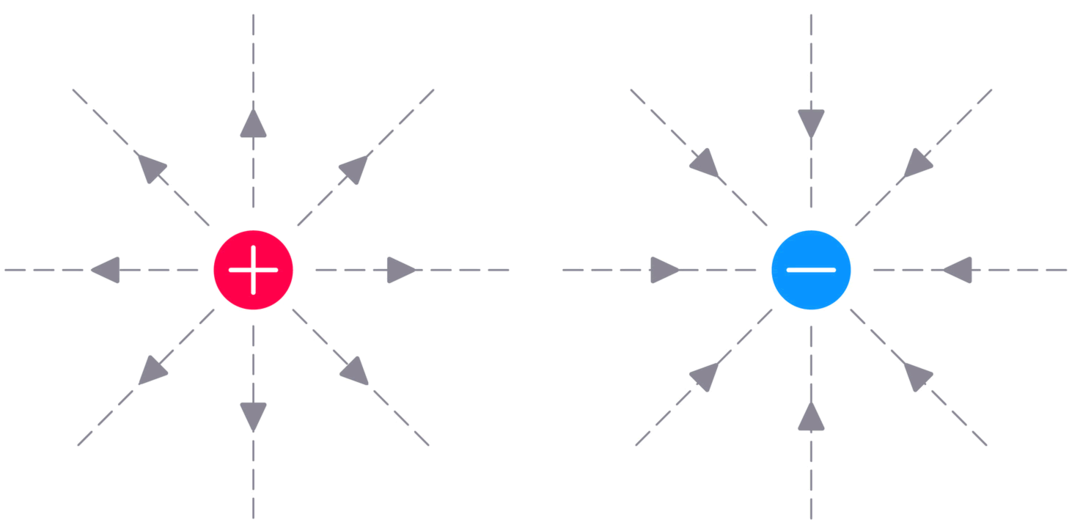
Illustration 1. From Studiowork.- Diagram of the electric fields generated by two point charges, one positive and one negative.

This law owes its name to the mathematician Johann Carl Friedrich Gauss who formulated it based on his divergence theorem.

Gauss's law for the magnetic field

\(\nabla \cdot \vec{B}=0\)

Gauss's law for the magnetic field

This law does not have a specific name, but it is called that because of its similarity to the previous equation. The meaning of this expression is that there is no "magnetic charge" analogous to "electric charge", that is, there are no magnetic monopoles that are the source of the magnetic field. This is the reason why if we break a magnet in half we will still have two similar magnets, both with a north pole and a south pole.

Faraday's Law

\(\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\)
Faraday's law of induction

This is the famous law of induction formulated by Faraday when in 1831 he discovered that changing magnetic fields were capable of inducing electric currents. What this equation means is that a magnetic field that changes with time is capable of inducing around it an electric field, which in turn can cause electric charges to move and create a stream. Although this may sound very abstract at first, Faraday's law is behind the workings of motors, electric guitars, and induction cooktops.

Ampère–Maxwell law

\(\nabla \times \vec{B}={{\mu }_{0}}\vec{J}+{{\mu }_{0}}{{\epsilon }_{0}}\frac {\partial \vec{E}}{\partial t}\)

The first thing this equation tells us is that electric currents generate magnetic fields around the direction of the current and that the magnitude of the generated magnetic field depends on the magnitude of this, this was what Oersted observed and that later Ampère was able to formulate. However, there is something curious behind this equation, and that is that the second term on the side law of the equation was introduced by Maxwell because this expression was originally inconsistent with the others, in particular, it led to a violation of the law of conservation of electric charge. To avoid this Maxwell simply introduced this second term so that all of his theory would be consistent, this term received the name of "displacement current" and at the time there was no experimental evidence to support it. will back up

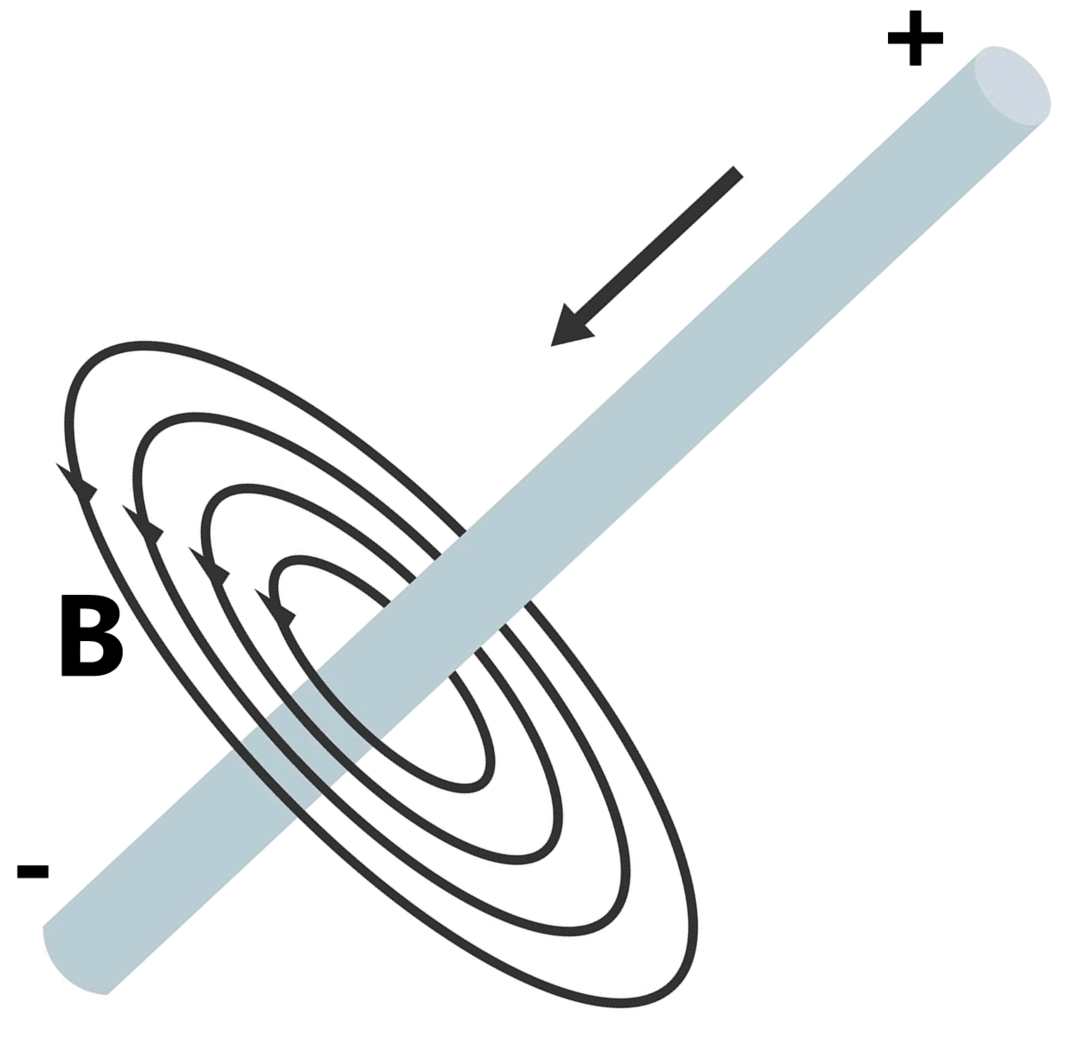
Illustration 2. De Rumruay.- An electric current flowing through a cable generates a magnetic field around it according to Ampère's Law.

The meaning of the displacement current is that, in the same way that a magnetic field variable induces an electric field, an electric field that changes with time is capable of generating a field magnetic. The first experimental confirmation of the displacement current was the demonstration of the existence of electromagnetic waves by Heinrich Hertz in 1887, more than 20 years after the publication of the theory of Maxwell. However, the first direct measurement of displacement current was made by M. R. Van Cauwenberghe in 1929.

light is an electromagnetic wave

One of the first mind-boggling predictions made by Maxwell's equations is the existence of electromagnetic waves, but not only that, they also revealed that light had to be a wave of this Type. To see this somewhat we will play around with Maxwell's equations a bit, but before that, here is the form of any wave equation:

\({{\nabla }^{2}}u=\frac{1}{{{v}^{2}}}\frac{{{\partial }^{2}}u}{\partial {{ t}^{2}}}\)
General form of a wave equation in three dimensions.

Where \({{\nabla }^{2}}\) is the Laplacian operator, \(u\) is a wave function, and \(v\) is the speed of the wave. We will also work with Maxwell's equations in empty space, that is, in the absence of electric charges and electric currents, only electric and magnetic fields:

\(\nabla \cdot \vec{E}=0\)

\(\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\)

\(\nabla \cdot \vec{B}=0\)

\(\nabla \times \vec{B}={{\mu }_{0}}{{\epsilon }_{0}}\frac{\partial \vec{E}}{\partial t}\)

And we will also use the following identity vector calculus:

\(\nabla \times \left( \nabla \times \vec{A} \right)=\nabla \left( \nabla \cdot \vec{A} \right)-{{\nabla }^{2}} \time{A}\)

If we apply this identity to electric and magnetic fields using Maxwell's equations for empty space above, we get the following results:

\({{\nabla }^{2}}\vec{E}={{\mu }_{0}}{{\epsilon }_{0}}\frac{{{\partial }^{2} }\vec{E}}{\partial {{t}^{2}}}\)

\({{\nabla }^{2}}\vec{B}={{\mu }_{0}}{{\epsilon }_{0}}\frac{{{\partial }^{2} }\vec{B}}{\partial {{t}^{2}}}\)

Note the similarity of these equations to the wave equation above, in conclusion, electric and magnetic fields can behave like waves (electromagnetic waves). If we define the speed of these waves as \(c\) and compare these equations with the wave equation above we can say that the speed is:

\(c=\frac{1}{\sqrt{{{\mu }_{0}}{{\epsilon }_{0}}}}\)

\({{\mu }_{0}}\) and \({{\epsilon }_{0}}\) are the magnetic permeability and electrical permittivity of vacuum, respectively, and both are constants universals whose values ​​are \({{\mu }_{0}}=4\pi \times {{10}^{-7}}~~T\cdot m/A\) and \({{\epsilon } 0}}=8.8542\times {{10}^{-12}}~{{C}^{2}}/N\cdot m~\), substituting these values, we have that the value of \(c\) is \(c=299,792,458\frac{m}{s}\approx 300,000~km/s\) which is exactly the speed of the light.

With this small analysis we can obtain three very important conclusions:

1) Electric and magnetic fields can behave like waves, that is, there are electromagnetic waves that are also capable of propagating through a vacuum.

2) Light is an electromagnetic wave whose speed depends on the magnetic permeability and permittivity light of the medium through which it propagates, in empty space light has a speed of approximately 300,000 km/s.

3) Since the magnetic permeability and the electrical permittivity are universal constants, then the speed of light is also a universal constant, but this also implies that its value does not depend of framework from which it is measured.

This last statement was highly controversial at the time. How is it possible that the speed of light is the same regardless of the movement of the person measuring it and the movement of the light source. light? The speed of something has to be relative, right? Well, this was a watershed for the physics of the time and this simple but profound fact led to the development of the Theory of Special Relativity by Albert Einstein in 1905.