Quadratic Function Definition

A quadratic function of a real variable whose form is expressed.

\(f\left( x \right) = a{x^2} + bx + c\)

Where the variable is \(x\), \(a, b\) and c are real constants, called coefficients of the quadratic function with \(a \ne 0.\)

The table advances general examples of quadratic functions and the situation they can model, to later illustrate their direct application from real problems.

Quadratic function	Situation you can model
\(f\left( x \right) = {x^2}\)	The variable \(y\) is the area of ​​a square whose side measures \(x\).
\(f\left( x \right) = \pi {x^2}\)	The variable \(y\) is the area of ​​a circle whose radius is \(x\).
\(f\left( x \right) = 100 – 4.9{x^2}\)	The variable \(y\) is the height of an object that was dropped at a height of 100 and \(x\) is the elapsed time.
\(f\left( x \right) = 60\left( {{\bf{sin}}45^\circ } \right) x – 4.9{x^2}\)	The variable \(y\) is the height of a cannonball thrown at an angle of 45° with a velocity of 60 m/s and \(x\) is the elapsed time.

The general formula and the quadratic function

If for \(x = \alpha \) the quadratic function is zero, then the number is \(\alpha \) is called the root of the quadratic function, yes, \(\alpha \) is the solution of the quadratic equation

\(a{x^2} + bx + c = 0\)

The general formula to solve quadratic equations we have that the roots of a quadratic function are:

\(\alpha = \frac{{ – b + \sqrt {{b^2} – 4ac} }}{{2a}},\;\;\beta = \frac{{ – b – \sqrt {{b ^2} – 4ac} }}{{2a}}\)

From the above, the following relationship between the roots and the coefficients of the quadratic function is established:

\(\alpha + \beta = – \frac{b}{a},\;\;\alpha \beta = \frac{c}{a}\)

Through notable products the following identity is established:

\(a{x^2} + bx + c = a\left( {x – \alpha } \right)\left( {x – \beta } \right)\)

In a similar way to that established in the general formula, it is established that the quadratic function can be expressed in the form:

\(f\left( x \right) = a{\left( {x – h} \right)^2} + k\)

With \(h = – \frac{b}{{2a}}\) and \(k = – \frac{{{b^2} – 4ac}}{a}\)

By solving the equation:

\(a{\left( {x – h} \right)^2} + k = 0\)

Is obtained:

\(\left| {x – h} \right| = \sqrt { – \frac{k}{a}} \)

\(x = h \pm \sqrt { – \frac{k}{a}} \)

From the above it can be concluded that \(f\left( x \right) = a{\left( {x – h} \right)^2} + k\), only if the constants \(k\) and \(a\) are of opposite signs, this quadratic function has real roots, which are: \(h + \sqrt { – \frac{k}{a}} ,\;\;h – \sqrt { – \frac{k}{a} } \).

If the constants \(k\) and \(a\) have the same sign then the quadratic function has no real roots.

When \(k = 0,\;\;\)the quadratic function has only one root.

Examples applied to real life

Application example 1: Economics

A school wants to organize a soccer tournament where each team plays each of the other teams only once. There is a budget of $15,600 for the cost of arbitration, if the cost of arbitration is $200 per game. How many teams can register for the tournament?

Problem statement: We must find a function that calculates the number of matches when we have \(n\) teams to count them we will make the assumption that team 1 plays first with all the others, that is \(n – 1\) matches. Team 2 would now play with all the rest, that is, with \(n – 2\), since they will have already played with team 1. Team 3 will have already played with teams 1 and 2, so they would have to play with n-3 teams.

With the above reasoning we arrive at:

\(f\left( n \right) = n – 1 + n – 2 + \ldots + 2 + 1\)

\(f\left( n \right) = \frac{{n\left( {n – 1} \right)}}{2}\)

The cost function is:

\(C\left( n \right) = 200f\left( n \right) = 100n\left( {n – 1} \right)\)

Having a budget of $15,600, we have the equation:

\(100n\left( {n – 1} \right) = 15600\)

solution of the equation

\(100n\left( {n – 1} \right) = 15600\) Initial situation
\(n\left( {n – 1} \right) = 156\) Divide each side of the equation by 100
\({n^2} – n – 156 = \) Add \( – 156\) to each side of the equation
\(\left( {n – 13} \right)\left( {n + 12} \right) = 0\) We have \(\left( { – 13} \right)\left( {12} \right ) = – 156\) and \( – 13 + 12 = – 1\)
It was factored.
Solutions of the equation \(n = – 12,\;13\)
Answer: The budget is enough for 13 teams to register.

Application example 2: Economics

A metropolitan bus company has observed that, in an eight-hour day, each of its buses transports an average of 1,000 passengers. To be in a position to give your workers a raise, you'll need to increase your fare, which is currently $5; An economist calculates that, for each peso that the fare increases, each truck will lose an average of 40 passengers each day. The company has calculated that, to cover the salary increase, it must obtain an additional $760 per truck each day. How much must the fare increase?

Statement of the problem: Let \(x\) be the amount of pesos in which the ticket will rise, for which \(5 + x\) is the new cost of the ticket. With this same increase, each truck will transport \(1000 – 40x\) passengers per day, on average.

Finally, the revenue per truck is:

\(I\left( x \right) = \left( {5 + x} \right)\left( {1000 – 40x} \right) = – 40\left( {x + 5} \right)\left( {x – 25} \right)\)

In order to cover the salary increase, each bus must collect: \(1000\left( 5 \right) + 760 = 5760\)

Finally we have the equation:

\( – 40\left( {x + 5} \right)\left( {x – 25} \right) = 5760\)

solution of the equation
\( – 40\left( {x + 5} \right)\left( {x – 25} \right) = 5760\) Initial situation
\(\left( {x + 5} \right)\left( {x – 25} \right) = – 144\) Divide by \( – 40\) each side of the equation
\({n^2} – 20n – 125 = – 144\) The remarkable product was developed
\({n^2} – 20n + 19 = 0\) 144 were added to each
\(\left( {n – 19} \right)\left( {n – 1} \right) = 0\) We have \(\left( { – 19} \right)\left( { – 1} \ right) = 19\) and \( – 19 – 1 = – 20\)
factored
Solutions of the equation \(n = 1.19\)
Answer: The ticket price can go up $1 or $19 pesos.

Application example 3: Economics

A bread store sells an average of 1,200 rolls a week for $6 each. One day he decided to raise the price to $9 a piece; now her sales have decreased: she only sells an average of 750 rolls a week. What should be the price of each bun so that the revenue of the outlet is the highest possible? Assume that there is a linear relationship between demand and price.

Problem statement: Assuming that there is a linear relationship between demand D and price \(x,\) then

\(D = mx + b\)

When \(x = 6;D = 1200;\;\) which generates the equation:

\(1200 = 6m + b\)

When \(x = 9;D = 750;\;\) lo and the equation is obtained:

\(750 = 9m + b\)

Solving the system of equations, the relationship between demand and price is:

\(D = – 150x + 2100 = – 150\left( {x – 14} \right)\)

The income is equal to

\(I\left( x \right) = Dx = – 150x\left( {x – 14} \right)\)

Solution

The graph of income in a parabola that opens downward and its maximum value is reached at the vertex on which can be found by averaging the roots of the quadratic function that models the income. The roots are \(\alpha = 0,\;\;\beta = 14\).

\(h = \frac{{0 + 14}}{2} = 7\)

\(I\left( h \right) = – 150\left( 7 \right)\left( {7 – 14} \right) = 7350\)

Answer

The maximum revenue is $7,350 and is achieved with a price of $7; selling, on average, 1050 rolls a week.

Application example 4: Economics

The cost to manufacture \(n\) chairs in one day can be calculated with the quadratic function:

\(C\left( n \right) = {n^2} – 200n + 13000\)

Determine the minimum cost that can be achieved.

Problem Statement

The graph of \(C\left( n \right)\) is a parabola that opens upward and will reach its minimum point at \(h = – \frac{b}{{2a}} = – \frac{{\ left( { – 200} \right)}}{{2\left( 1 \right)}} = 100\)

\(C\left( {100} \right) = {\left( {100} \right)^2} – 200\left( {100} \right) + 13000 = 3000\)

Answer

The lowest possible cost is equal to $3000 and is achieved by manufacturing 100 chairs.

Application Example 5: Geometry

A rhombus has an area of ​​21 cm2; If the sum of the lengths of its diagonals is 17 cm, what is the length of each diagonal of the rhombus?

Problem statement: The area of ​​a rhombus is calculated with:

\(A = \frac{{Dd}}{2}\)

With \(D\) and \(d\) the lengths of its diagonals, it is also known:

\(D + d = 7\)

\(D = 17 – d\)

By substituting you get:

\(A = \frac{{\left( {17 – d} \right) d}}{2}\)

Finally we get the equation

\(\frac{{\left( {17 – d} \right) d}}{2} = 21\)

Solution
\(\frac{{\left( {17 – d} \right) d}}{2} = 21\) Initial situation
\(\left( {17 – d} \right) d = 42\) Multiply by \( – 40\) each side of the equation
\({d^2} – 17d + 42 = 0\) The product was developed.
\(\left( {d – 14} \right)\left( {d – 3} \right) = 0\) We have \(\left( { – 14} \right)\left( { – 3} \ right) = 42\) and \( – 14 – 3 = – 17\)
factored
Solutions of the equation \(d = 3.14\)
Answer:

The diagonals of the rhombus measure 14 cm and 3 cm.

Application Example 6: Geometry

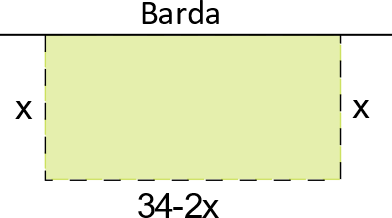
It is desired to build a rectangular chicken coop of 140 m2, taking advantage of a fairly long fence that will form the bottom of the chicken coop. The other three sides will be built with 34 linear meters of wire mesh, how much should the length and width of the chicken coop be to use the total mesh?

Under the same conditions, what is the maximum area that can be fenced with the same mesh?

Problem Statement: According to the diagram, the area is equal to:

\(A\left( x \right) = x\left( {34 – 2x} \right) = 2x\left( {17 – x} \right)\)

Where \(x\) is the length of the side perpendicular to the fence.

To know the measurements of the rectangle so that it has an area of ​​140 m2, it is enough to solve the equation

\(2x\left( {17 – x} \right) = 140\)

As the graph of \(A\left( x \right)\) is a parabola that opens downwards to calculate the maximum value of the area, it is enough to calculate the vertex of the parabola.

Answers
Measures of the rectangle with area 140 m2
Length of the side perpendicular to the fence

\(x\) Length of the side parallel to the fence

\(34 – 2x\)
10 14
7 20

The first coordinate of the vertex is \(h = \frac{{17}}{2}\) and

\(A\left( h \right) = \frac{{289}}{2}\)

The area is maximum when the perpendicular side measures \(\frac{{17}}{2}\;\)m and the parallel side measures 17m, it measures 17m, the value of the maximum area reached is \(\frac{{289}} {2}\)m2.

Graph of a quadratic function

From a geometric point of view, the roots are the points where the graph of a function intersects the \(x\) axis.

From the expression

\(f\left( x \right) = a{\left( {x – h} \right)^2} + k,\)

We will establish the general form of the graph of a quadratic function.

First case \(a > 0\) and \(k > 0\)

\(f\left( x \right) = a{\left( {x – h} \right)^2} + k\)

\(x\)	\(f\left( x \right)\)
\(h – 1\)	\(a + k\)
\(h – 2\)	\(4a + k\)
\(h – 3\)	\(9a + k\)
\(h – 4\)	\(16a + k\)
\(h\)	\(k\)
\(h + 1\)	\(a + k\)
\(h + 2\)	\(4a + k\)
\(h + 3\)	\(9a + k\)
\(h + 4\)	\(16a + k\)

In this case the graph satisfies:

Symmetric: With axis of symmetry \(x = h = – \frac{b}{{2a}}.\) That is \(f\left( {h – s} \right) = f\left( {h + s} \right)\)

It is above the \(x\) axis and does not intersect it. That is, \(f\left( x \right) > 0\) has no real roots.

The lowest point on the graph is at point \(\left( {h, k} \right)\). That is \(f\left( x \right) \ge f\left( h \right) = k\)

Second case \(a < 0\) and \(k < 0\)

\(f\left( x \right) = a{\left( {x – h} \right)^2} + k\)

\(x\)	\(f\left( x \right)\)
\(h – 1\)	\(a + k\)
\(h – 2\)	\(4a + k\)
\(h – 3\)	\(9a + k\)
\(h – 4\)	\(16a + k\)
\(h\)	\(k\)
\(h + 1\)	\(4a + k\)
\(h + 2\)	\(9a + k\)
\(h + 3\)	\(4a + k\)
\(h + 4\)	\(16a + k\)

In this case the graph satisfies:

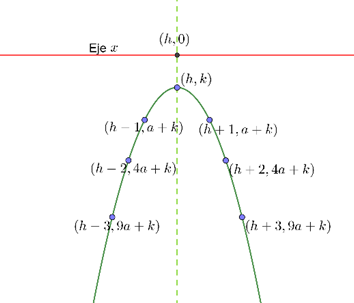
Symmetric: With axis of symmetry \(x = h = – \frac{b}{{2a}}.\) That is \(f\left( {h – s} \right) = f\left( {h + s} \right)\)

It is below the \(x\) axis and does not intersect it. That is, \(f\left( x \right) < 0\) has no real roots. The highest point on the graph is at point \(\left( {h, k} \right)\). That is \(f\left( x \right) \le f\left( h \right) = k\) Third case \(a > 0\) and \(k \le 0\).

This case is similar to the first case, the difference is that now we have one real root (when \(k = 0\) ) or two real roots.

In this case the graph satisfies:

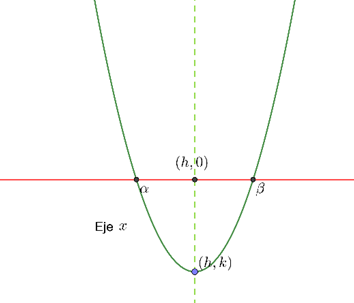
Symmetric: With axis of symmetry \(x = h = – \frac{b}{{2a}}.\) That is \(f\left( {h – s} \right) = f\left( {h + s} \right)\)

It intersects the \(x\) axis, that is, it has at least one real root.

The lowest point on the graph is at point \(\left( {h, k} \right)\). That is \(f\left( x \right) \ge f\left( h \right) = k\)

Fourth case \(a < 0\) and \(k \ge 0\). This case is similar to the second case, the difference is that now we have one real root (when \(k = 0\) ) or two real roots. In this case the graph satisfies:

Symmetric: With axis of symmetry \(x = h = – \frac{b}{{2a}}.\) That is \(f\left( {h – s} \right) = f\left( {h + s} \right)\)

The lowest point on the graph is at point \(\left( {h, k} \right)\). That is \(f\left( x \right) \le f\left( h \right) = k\)

The graph of a quadratic function is called a parabola and its elements to highlight are the axis of symmetry, the points where it intersects to the \(x\) axis and the vertex, which is the point on the graph of the function where it reaches its lowest or highest point depending on the case.

Based on the analysis carried out, we can state:

The parabola associated with the quadratic function \(f\left( x \right) = a{x^2} + bx + c\) has its vertex at \(\left( {h, k} \right)\) where :

\(h = – \frac{b}{{2a}},\;\;k = f\left( h \right)\)

examples

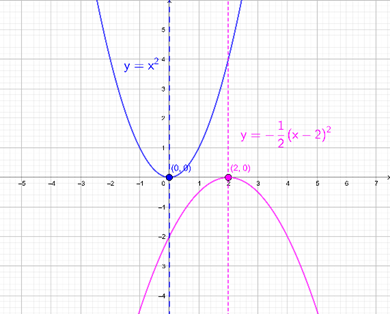
Quadratic function \(y = {x^2}\)	important elements
Vertex of the parabola	\(\left( {0,0} \right)\)
Axis of symmetry of the parabola	\(x = 0\)
Intercepts with the \(x\) axis	\(\left( {0,0} \right)\)

Quadratic function \(y = – \frac{1}{2}{\left( {x – 2} \right)^2}\)	important elements
Vertex of the parabola	\(\left( {2,0} \right)\)
Axis of symmetry of the parabola	\(x = 2\)
Intercepts with the \(x\) axis	\(\left( {2,0} \right)\)

Quadratic function \(y = {\left( {x + 2} \right)^2} – 4\)	important elements
Vertex of the parabola	\(\left( { – 2, – 4} \right)\)
Axis of symmetry of the parabola	\(x = – 2\)
Intercepts with the \(x\) axis	\(\left( { – 4,0} \right);\left( {0,0} \right)\)

Quadratic function \(y = – \frac{1}{2}{\left( {x – 9} \right)^2} + 8\)	important elements
Vertex of the parabola	\(\left( {9,8} \right)\)
Axis of symmetry of the parabola	\(x = 9\)
Intercepts with the \(x\) axis	\(\left( {5,0} \right);\left( {13,0} \right)\)

Quadratic function \(y = {x^2} + 1\)	important elements
Vertex of the parabola	\(\left( {0,1} \right)\)
Axis of symmetry of the parabola	\(x = 0\)
Intercepts with the \(x\) axis	Does not have

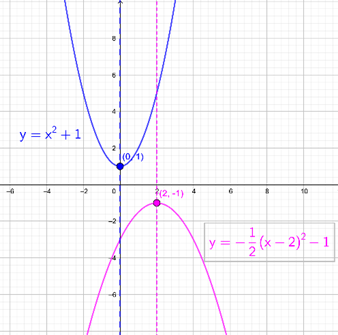
Quadratic function \(y = – \frac{1}{2}{\left( {x – 2} \right)^2} – 1\)	important elements
Vertex of the parabola	\(\left( {2, – 1} \right)\)
Axis of symmetry of the parabola	\(x = 2\)
Intercepts with the \(x\) axis	Does not have

If the real roots of a quadratic function exist, we can graph its associated parabola from them. Suppose that \(f\left( x \right) = a\left( {x – \alpha } \right)\left( {x – \beta } \right)\)

For this, the following must be taken into account:

\(\alpha + \beta = – \frac{b}{a}\)

\(\frac{{\alpha + \beta }}{2} = – \frac{b}{{2a}} = h\)

As

\(k = f\left( h \right)\)

\(k = f\left( {\frac{{\alpha + \beta }}{2}} \right)\)

\(k = a\left( {\frac{{\alpha + \beta }}{2} – \alpha } \right)\left( {\frac{{\alpha + \beta }}{2} – \ beta } \right)\)

\(k = – \frac{a}{4}{\left( {\alpha – \beta } \right)^2}\)

examples

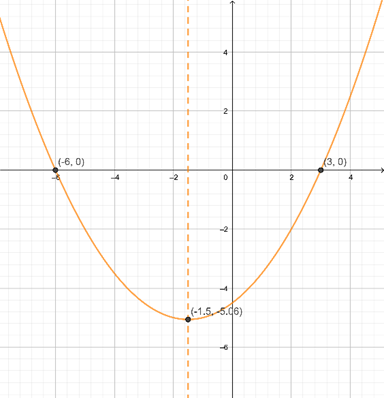
Sketch the graph of the quadratic function \(f\left( x \right) = \frac{1}{4}\left( {x – 3} \right)\left( {x + 6} \right )\)

Solution

The roots are \(\alpha = 3\;\) and \(\beta = – 6\); then \(h = \frac{{3 – 6}}{2} = – \frac{3}{2}\).

\(k = f\left( { – \frac{3}{2}} \right) = 2\left( { – \frac{3}{2} – 3} \right)\left( { – \frac {3}{2} + 6} \right) = \frac{1}{4}\left( { – \frac{9}{2}} \right)\left( {\frac{9}{2}} \right) = – \frac{{81}}{{16}}\)

So we can build the following table

\(f\left( x \right) = 2\left( {x – 3} \right)\left( {x + 6} \right)\)	important elements
Vertex of the parabola	\(\left( { – \frac{3}{2}, – \frac{{81}}{2}} \right)\)
Axis of symmetry of the parabola	\(x = – \frac{{81}}{2}\)
Intercepts with the \(x\) axis	\(\left( { – 6,0} \right)\;,\;\left( {3,0} \right)\)

To sketch the graph of the function:

\(f\left( x \right) = 3{x^2} – 18x + 4\)

We will use the same ideas that we have already used; For this we will first determine the vertex.

In this case, \(a = 3;b = – 12,\;c = 4\).

Since \(a > 0\), the parabola “will open up and \(h = – \frac{b}{{2a}} = – \left( {\frac{{ – 18}}{{3\left ( 2 \right)}}} \right) = 3.\) Next we will calculate \(k:\)

\(k = f\left( h \right) = f\left( 3 \right) = 3{\left( 3 \right)^2} – 18\left( 3 \right) + 4 = – 23\)

The vertex of the parabola is at \(\left( {3, – 23} \right)\) and since it opens upwards, then the parabola will intersect the \(x\;\) axis and its axis of symmetry is \(x = 3\).

Now let us consider the quadratic function

\(f\left( x \right) = – 5{x^2} + 10x – 9\)

In this case, \(a = 3;b = – 12,\;c = 4\).

Since \(a < 0\), the parabola will “open” downward and \(h = - \frac{b}{{2a}} = - \left( {\frac{{10}}{{\left( 2 \right)\left( { - 5} \right)}}} \right) = 1.\) A Next we will calculate \(k:\) \(k = f\left( h \right) = f\left( 1 \right) = - 5{\left( 1 \right)^2} + 10\left( 1 \ right) - 9 = - 4\) The vertex of the parabola is at \(\left( {1, - 4} \right)\) and since it opens downward, then the parabola will not intersect the \(x\;\) axis and its axis of symmetry is \(x = 1.\)