What is Cronbach's Alpha and how is it defined?

Marco Antonio Villanueva Bustamante
PhD in Psychology

Cronbach's alpha is the most widely used coefficient to estimate the internal consistency of a measurement scale.

One of the fundamental elements when building and using a scale is reliability, this is defined as the stability presented by a measuring instrument, when it is applied on multiple occasions while conditions are present Similar. In other words, reliability indicates how accurate a measurement instrument is by evaluating the construct of interest on more than one occasion. To assess reliability, multiple techniques can be used, such as the test-retest coefficient that establishes the correlation between the response of a measuring instrument that is applied on two different occasions; the coefficient of parallel forms, is calculated by applying an instrument that has two different versions; finally, the coefficient of internal consistency which does not require more than one measurement, this coefficient can be calculated by various methods, but Cronbach's Alpha is the most common.

Cronbach's alpha is proposed by Lee J. Cronbach in 1951, as a measure against the limitation of the KR-20 and KR-21 coefficient developed by Kuder and Richardson, which can only be applied to scales that have response options dichotomous

To calculate Cronbach's alpha (α), the following formula is used:

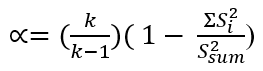
Where k is the number of test items; S_Yo² is the variance of the items and S_sum² is the total variance of the scale. In other words, alpha is obtained by calculating the correlation of each item on the scale with each of the other items, then it is average these correlations and the result would be the value of alpha, it is worth mentioning that these correlations are estimated by means of the correlation coefficient of pearson. Therefore, reliability through alpha is related to the length of the scale and the level of covariance (correlation) between its items. Cronbach's alpha value can be between 0 and 1, the closer to 1 represents the better internal consistency index; in this sense, the minimum acceptable value of alpha is .70 and values ​​greater than .90 would indicate redundancy in the items.

Cronbach's alpha has become the most widely used method to estimate the internal consistency of a scale, due to its advantages over other methods, but also because most statistical packages and programs can estimate this worth. However, the use of Cronbach's alpha is not without its critics, most of which stem from the violation of its assumptions.

Assumptions of Cronbach's Alpha

1. Tau equivalence, this refers to the fact that all the items of a scale measure the same trait or the same latent factor with a similar degree of precision.
2. The errors must not be correlated, since it is assumed that they are independent.
3. Unidimensionality of the items, that is, the items of a scale must measure a single latent trait.
4. The measurement level of the operationalized variable must be continuous.

Failure to comply with any of these assumptions may cause an erroneous estimate in the Cronbach's Alpha values. However, given the nature of the data in the social and health sciences, it is common not to meet the fourth assumption; that is, the data tend to be ordinal. Applying the alpha coefficient to ordinal data, especially when there are less than 5 response options, can cause an underestimation of the values. For this reason, alternatives have emerged for Cronbach's Alpha.

The Ordinal Alpha

The estimation of internal consistency using the ordinal alpha follows the same logic as Cronbach's Alpha, with the difference, that instead of using the Pearson correlation matrix, ordinal alpha uses the polychoric correlation matrix or tetrachoric. Similarly, unlike Cronbach's alpha which is sensitive to data skewness, ordinal alpha is an unbiased estimate.

McDonald's Omega

Given the breach of the assumption of equivalence between the items, the McDonald omega is a method for estimating internal consistency that has been gaining relevance. Among the advantages of this coefficient are that unlike alpha, omega works with loads factors of each item and does not depend on the number of items on the scale, as can be seen in the following formula.

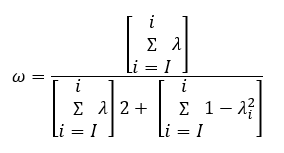
where λ is the loading factor and λ_i is the loading factor, standardized. Similar to Cronbach's alpha, omega values ​​between .70 and .90 represent adequate values.

Despite the advantages represented by the use of McDonald's ordinal alpha and omega, its application in research is still scarce, This may be because most statistical software and packages do not yet have an option to esteem them.