Definition of Equivalent Fractions

Two or more fractions are said to be equivalent if they represent the same quantity, that is, if
\(\frac{a}{b} = \frac{c}{d}\;,\)
the fractions \(\frac{a}{b}\) and \(\frac{c}{d}\) are said to be equivalent.

Equivalent Fractions: Graphic Representation

Consider the square, which we will divide into fourths, thirds, eighths, and twelfths.

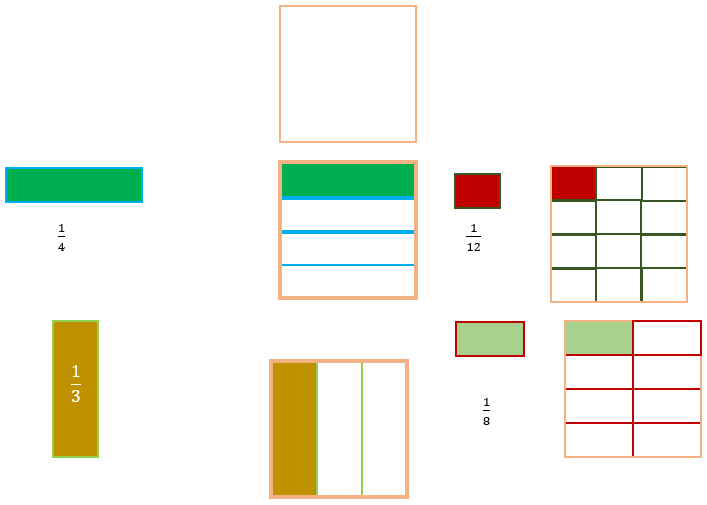
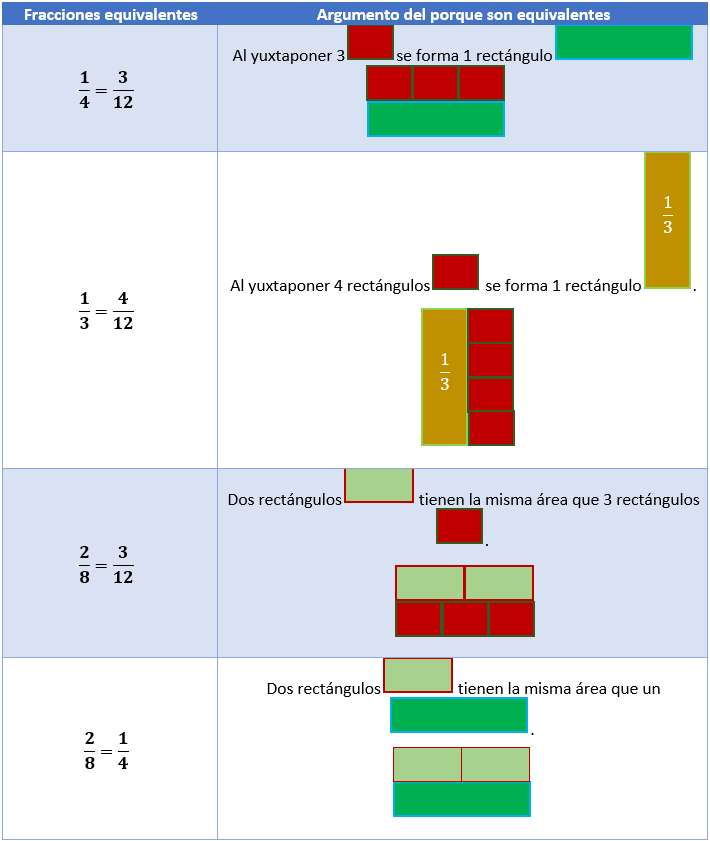
From the previous figures we notice the following equivalences:

How to obtain one or several equivalent fractions?

There are two basic methods for obtaining a fraction equivalent to a given fraction.

1. Multiply the numerator and denominator by the same positive number.

Examples:

\(\frac{3}{4} = \frac{{3\left( 5 \right)}}{{4\left( 5 \right)}} = \frac{{15}}{{20}} \)

\(\frac{3}{4} = \frac{{3\left( 7 \right)}}{{4\left( 7 \right)}} = \frac{{21}}{{28}} \)

\(\frac{5}{8} = \frac{{5\left( 6 \right)}}{{8\left( 6 \right)}} = \frac{{30}}{{56}} \)

2. It is divided by the same positive common divisor of the numerator and denominator.

\(\frac{{52}}{{56}} = \frac{{52 \div 4}}{{56 \div 4}} = \frac{{13}}{{14}}.\)

\(\frac{{80}}{{140}} = \frac{{80 \div 20}}{{140 \div 20}} = \frac{4}{7}.\)

\(\frac{{21}}{{57}} = \frac{{21 \div 3}}{{57 \div 3}} = \frac{7}{{19}}\)

When in a fraction both the numerator and the denominator are divided by the same common divisor other than 1, it is said that the fraction has been reduced.

irreducible fractions

A fraction is called an irreducible fraction if the greatest common divisor of the numerator and denominator is equal to 1.

If \(gcd\left( {a, b} \right) = 1,\) the fraction \(\frac{a}{b}\) is called an irreducible fraction.

Given a fraction \(\frac{a}{b}\) to obtain a fraction equivalent to this fraction and which is also an irreducible fraction the numerator and numerator are divided by the greatest common divisor of \(a\;\) and of \(b.\)

The following table shows examples of irreducible and reducible fractions; if it is reducible, it shows how to obtain an irreducible equivalent fraction.

Fraction	Greatest common divisor	Irreducible	irreducible equivalent fraction
\(\frac{{14}}{{42}}\)	7	No	\(\frac{{14}}{{42}} = \frac{{14 \div 7}}{{42 \div 7}} = \frac{2}{7}\)
\(\frac{3}{{25}}\)	1	Yeah	\(\frac{3}{{25}}\)
\(\frac{{21}}{{201}}\)	3	No	\(\frac{{21 \div 3}}{{20\;1 \div 3}} = \frac{7}{{67}}\)
\(\frac{5}{{24}}\)	1	Yeah	\(\frac{5}{{24}}\)
\(\frac{{72}}{{1125}}\)	9	No	\(\frac{{72}}{{1125}} = \frac{{72 \div 9}}{{1125 \div 9}} = \frac{8}{{125}}\)

Equivalent fractions: verbal representation.

The following table shows two different ways to display equivalent information, from the numerical point of view.

Verbal phrase	Equivalent phrase (numerically)	Argumentation
In 1930, in Mexico, 4 people out of 25 people spoke a native language.	In 1930, in Mexico, 16 people out of 100 people spoke a native language.	Both data were multiplied by 4
In 1960, in Mexico, 104 people out of every 1,000 people spoke a native language.	In 1960, in Mexico, 13 people out of 125 people spoke a native language	Both data were divided by 8.

Equivalent Fractions: Decimal Representation

The table below shows various decimal numbers and equivalent fractions that represent them.

Decimal number	Fraction	equivalent fraction	Operations
\(0.25\)	0.25=\(\frac{{25}}{{100}}\)	0.25=\(\frac{1}{4}\)	\(25 \div 25 = 1\) \(100 \div 25 = \)
\(1.4\)	\(1.4 = 1 + \frac{4}{{10}} = \frac{{14}}{{10}}\)	\(1.4 = \frac{7}{5}\)	\(14 \div 2 = 1\) \(10 \div 2 = 5\)
\(0.145\)	\(0.145 = \frac{{145}}{{1000}}\)	\(0.145 = \frac{{29}}{{200}}\)	\(145 \div 5 = 29\) \(1000 \div 5 = 200\)

Equivalent Fractions: Representation as a Percent

The table below shows various decimal numbers and equivalent fractions that represent them.

Decimal number	Fraction	equivalent fraction	Operations
20%	\(\frac{{20}}{{100}}\)	\(\frac{1}{5}\)	\(20 \div 20 = 1\) \(100 \div 20 = 5\)
150%	\(\frac{{150}}{{100}}\)	\(\frac{3}{2}\)	\(150 \div 50 = 3\) \(100 \div 50 = 2\)
55%	\(\frac{{55}}{{100}}\)	\(\frac{{11}}{{20}}\)	\(55 \div 11 = 5\) \(100 \div 5 = 20\)

Equivalent Fractions: From Heterogeneous to Homogeneous

Given two heterogeneous fractions \(\frac{a}{b}\) and \(\frac{c}{d}\), we can find two fractions homogeneous in such a way that one fraction is equivalent to the fraction \(\frac{a}{b}\;\) and the other to \(\frac{c}{d}\).

Next, we will show two procedures to perform what is mentioned in the previous paragraph.

Let's observe:

\(\frac{a}{b} = \frac{{a\left( d \right)}}{{b\left( d \right)}}\)

\(\frac{c}{d} = {\rm{\;}}\frac{{c\left( b \right)}}{{d\left( b \right)}}\)

The following table shows some examples.

F. heterogeneous	Operations	F. homogeneous
\(\frac{4}{5}\), \(\frac{2}{3}\)	\(\frac{{4\left( 3 \right)}}{{5\left( 3 \right)}} = \frac{{12}}{{15}}\) \(\frac{{2\left( 5 \right)}}{{3\left( 5 \right)}} = \frac{{10}}{{15}}\)	\(\frac{{12}}{{15}}\), \(\frac{{10}}{{15}}\)
\(\frac{7}{{12}}\), \(\frac{4}{{18}}\)	\(\frac{{7\left( {18} \right)}}{{12\left( {18} \right)}} = \frac{{126}}{{216}}\) \(\frac{{4\left( {12} \right)}}{{18\left( {12} \right)}} = \frac{{48}}{{216}}\)	\(\frac{{126}}{{216}},\) \(\frac{{48}}{{216}}\)
\(\frac{7}{{10}}\), \(\frac{3}{{14}}\), \(\frac{5}{4}\)	\(\frac{{7\left( {14} \right)\left( 4 \right)}}{{10\left( {14} \right) 4}} = \frac{{392}}{{ 560}}\) \(\frac{{3\left( {10} \right)\left( 4 \right)}}{{14\left( {10} \right)\left( 4 \right)}} = \frac{ {120}}{{560}}\) \(\frac{{5\left( {10} \right)\left( {14} \right)}}{{4\left( {10} \right)\left( {14} \right)}} = \frac{{700}}{{560}}\)	\(\frac{{392}}{{560}}\), \(\frac{{120}}{{560}},\) \(\frac{{700}}{{560}}\)

The disadvantage of this method is that very large numbers can be produced in the process; In many cases it is possible to avoid it, if the least common multiple of the denominators is calculated and the second method is based on the calculation of the least common multiple.

Least common multiple in calculating fractions

Next, through two examples, how to obtain homogeneous fractions using the least common multiple of the denominators, which will be the common denominator of the fractions involved.

Consider the fractions: \(\frac{7}{{12}}\), \(\frac{4}{{18}}.\)

The least common multiple of \(12\) and \(18\) is \(36\); now

\(36 \div 12 = 3\)

\(36 \div 18 = 2\)

\(\frac{7}{{12}} = \frac{{7\left( 3 \right)}}{{12\left( 3 \right)}} = \frac{{21}}{{36 }},\)

\(\frac{4}{{18}} = \frac{{4\left( 2 \right)}}{{18\left( 2 \right)}} = \frac{8}{{36}} \)

Now consider the fractions: \(\frac{7}{{10}}\), \(\frac{3}{{14}}\), \(\frac{5}{4}\)

The least common multiple of \(10\), \(14\) and \(3\) is \(140\); now

\(140 \div 10 = 14\)

\(140 \div 14 = 10\)

\(140 \div 4 = 35\)

\(\frac{7}{{10}} = \frac{{7\left( {14} \right)}}{{10\left( {14} \right)}} = \frac{{98} }{{140}},\)

\(\frac{3}{{14}} = \frac{{3\left( {10} \right)}}{{14\left( {10} \right)}} = \frac{{30} }{{140}}\)

\(\frac{5}{4} = \frac{{5\left( {35} \right)}}{{4\left( {35} \right)}} = \frac{{175}}{ {140}}\)

From the previous figures we notice the following fact:

\(\frac{1}{4} = \frac{3}{{12}}\)

Here are other examples.

F. heterogeneous	min common denominators	Operations	F. homogeneous
\(\frac{1}{{14}}\) \(\frac{1}{{18}}\)	126	\(126 \div 14 = 9\) \(\frac{1}{{14}} = \frac{{1\left( 9 \right)}}{{14\left( 9 \right)}} = \frac{9}{{126}} \) \(126 \div 18 = 7\) \(\frac{1}{{18}} = \frac{{1\left( 7 \right)}}{{18\left( 7 \right)}} = \frac{7}{{126}} \)	\(\frac{9}{{126}}\), \(\frac{7}{{126}}\)
\(\frac{5}{6}\) \(\frac{2}{{15}},\) \(\frac{4}{9}\)	90	\(90 \div 6 = 15\) \(\frac{5}{6} = \frac{{5\left( {15} \right)}}{{6\left( {15} \right)}} = \frac{{75}}{ {90}}\) \(90 \div 15 = 6\) \(\frac{2}{{15}} = \frac{{2\left( {15} \right)}}{{15\left( 6 \right)}} = \frac{{30}}{ {90}}\) \(90 \div 9 = 10\) \(\frac{4}{9} = \frac{{4\left( {10} \right)}}{{9\left( {10} \right)}} = \frac{{40}}{ {90}}\)	\(\frac{{75}}{{90}}\), \(\frac{{30}}{{90}}\), \(\frac{{40}}{{90}}\)