Definition of Arithmetic Progression

A sequence of numbers \({a_1},\;{a_2},{a_3}, \ldots \) ​​is called an arithmetic progression if the difference between two consecutive numbers is equal to the same number \(d\), that is Yeah:

\({a_{n + 1}} - {a_n} = d\)

The number \(d\) is called the difference of the arithmetic progression.

The element \({a_1}\) is called the first element of the arithmetic sequence.

The elements of the arithmetic progression can be expressed in terms of the first element and its difference, that is:

\({a_1},{a_1} + d,{a_1} + 2d,{a_1} + 3d\)

They are the first four elements of the arithmetic progression; In general, the \(k – \)th element is expressed as follows:

\({a_k} = {a_1} + \left( {k – 1} \right) d\)

From the above expression we get:

\({a_k} – {a_l} = {a_1} + \left( {k – 1} \right) d – \left( {{a_1} + \left( {l – 1} \right) d} \right )\)

\({a_k} – {a_l} = \left( {k – l} \right) d\)

The above expression is equivalent to:

\({a_k} = {a_l} + \left( {k – l} \right) d\)

Examples applied for arithmetic progression

1. Find the difference of the arithmetic progression: \(3,8,13,18, \ldots \) ​​and find the elements \({a_{20}},\;{a_{99}}\)

Solution

Since \(5 = 8 – 3 = 13 – 8 = 18 – 3\) we can conclude that the difference is:

\(d = 5\)

\({a_{20}} = {a_1} + \left( {20 – 1} \right) d = 3 + 19\left( 5 \right) = 98\)

\({a_{99}} = {a_1} + \left( {99 – 1} \right) d = 3 + 98\left( 5 \right) = 493\)

2. In an arithmetic progression we have: \({a_{17}} = 20\;\)and \({a_{29}} = – 130\), determine the difference of the arithmetic progression and write the first 5 elements.

Solution

Wearing

\({a_k} – {a_l} = \left( {k – l} \right) d\)

\({a_{29}} – {a_{17}} = \left( {29 – 17} \right) d\)

\( – 130 – 20 = \left( {12} \right) d\)

\( – 150 = \left( {12} \right) d\)

\(12d = – 150\)

\(d = – \frac{{150}}{{12}} = – \frac{{25}}{2}\)

To find the first 5 elements; we will calculate \({a_1}\):

\({a_k} = {a_1} + \left( {k – 1} \right) d\)

\({a_{17}} = {a_1} + \left( {17 – 1} \right)\left( { – \frac{{25}}{2}} \right)\)

\(20 = {a_1} + \left( {16} \right)\left( { – \frac{{25}}{2}} \right)\)

\(20 = {a_1} – 200\)

\({a_1} = 20 + 200 = 220\)

The first 5 elements are:

\(220,220 + \left( { – \frac{{25}}{2}} \right),220 + 2\left( { – \frac{{25}}{2}} \right),220 + 3 \left( { – \frac{{25}}{2}} \right),220 + 4\left( { – \frac{{25}}{2}} \right)\)

\(220,\frac{{415}}{2},195,\frac{{365}}{2},170\)

Polygonal numbers and the sum of the first \(n\) elements of an arithmetic progression

triangular numbers

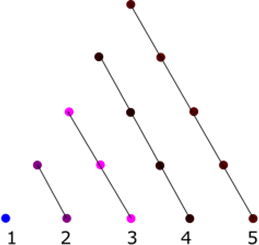
The triangular numbers \({T_n}\;\) are formed from the arithmetic progression: \(1,2,3,4 \ldots \); in the following way.

\({T_1} = 1\)

\({T_2} = 1 + 2 = 3\)

\({T_3} = 1 + 2 + 3 = 6\)

\({T_4} = 1 + 2 + 3 + 4 = 10\)

square numbers

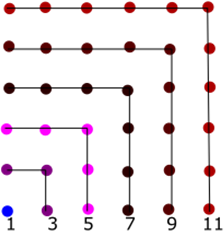
The square numbers \({C_n}\;\) are formed from the arithmetic progression: \(1,3,5,7 \ldots \); as follows

\({C_1} = 1\)

\({C_2} = 1 + 3 = 4\)

\({C_3} = 1 + 3 + 5 = 9\)

\(C{\;_4} = 1 + 3 + 5 + 7 = 16\)

pentagonal numbers

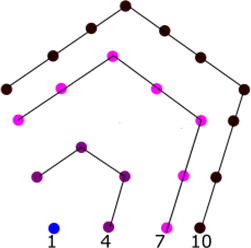
The square numbers \({P_n}\;\) are formed from the arithmetic progression: \(1,3,5,7 \ldots \); as follows

\({P_1} = 1\)

\({P_2} = 1 + 4 = 5\)

\({P_3} = 1 + 4 + 7 = 12\)

\({P_4} = 1 + 4 + 7 + 10 = 22\)

Next, we will show the formula to find the sum of the first \(n\) elements of an arithmetic progression.

Given the arithmetic progression, \({a_1},{a_2} = {a_1} + d,{a_3} + 2d, \ldots .,{a_n} = {a_1} + \left( {n – 1} \right) d\). To calculate the sum \({S_n} = {a_1} + {a_2} + {a_3} + \ldots + {a_n};\) you can use the formula:

\({S_n} = \frac{{n\left( {{a_1} + {a_n}} \right)}}{2}\)

which is equivalent to

\({S_n} = \frac{{n\left( {2{a_1} + \left( {n – 1} \right) d} \right)}}{2}\)

Applying the previous formula, the formulas to calculate the triangular, square and pentagonal numbers are obtained; which are shown in the following table.

polygonal number	\({a_1}\)	\(d\)	Formula
Triangular \(n – \)th	1	1	\({T_n} = \frac{{n\left( {n + 1} \right)}}{2}\)
Square \(n – \)th	1	2	\({C_n} = {n^2}\)
Pentagonal \(n – \)th	1	3	\({P_n} = \frac{{n\left( {3n – 1} \right)}}{2}\)

Example on polygonal numbers

3. From example 2 calculate \({S_{33}}\).

Solution

In this case \({a_1} = 200\) and \(d = – \frac{{25}}{2}\)

applying

\({S_n} = \frac{{n\left( {2{a_1} + \left( {n – 1} \right) d} \right)}}{2}\)

\({S_{33}} = \frac{{34\left( {2\left( {200} \right) + \left( {33 – 1} \right)\left( { – \frac{{25 }}{2}} \right)} \right)}}{2}\)

\({S_{33}} = 17\left( {400 + 16\left( { – 25} \right)} \right) = 17\left( 0 \right) = 0\)

arithmetic means

Given two numbers \(a\;\) and \(b,\) the numbers \({a_2},{a_3}, \ldots ,{a_{k + 1}}\) are called \(k\) means arithmetic numbers \(a\;\) and \(b\); if the sequence \(a,{a_2},{a_3}, \ldots ,{a_{k + 1}},b\) is an arithmetic progression.

To know the values ​​of the \(k\) arithmetic means of the numbers \(a\;\) and \(b\), it is enough to know the difference of the arithmetic progression, for this the following must be considered:

\(a = {a_1},{a_2},{a_3}, \ldots ,{a_{k + 1}},{a_{k + 2}} = b,\)

From the above we establish the relationship:

\(b = a + \left( {k + 2 – 1} \right) d\)

Solving for \(d\), we obtain:

\(d = \frac{{b – a}}{{k + 1}}\)

examples

4. Find 7 arithmetic means between the numbers -5 and 25.

Solution

When applying

\(d = \frac{{b – a}}{{k + 1}}\)

with \(b = 25,\;a = – 5\) and \(k = 7\;\):

\(d = \frac{{25 – \left( { – 5} \right)}}{{7 + 1}} = \frac{{30}}{8} = \frac{{15}}{4 }\)

The 7 arithmetic means are:

\( – \frac{5}{4},\;\frac{5}{2},\;\frac{{25}}{4},10,\frac{{55}}{4},\ frac{{35}}{2},\frac{{85}}{4}\)

9. One person gave $2,000 as a down payment to buy a refrigerator and paid the rest with his credit card for 18 months without interest. He must pay $550 a month to settle the debt, which he acquired to pay for his refrigerator.

to. What is the cost of the refrigerator?

b. If you have paid the rest over 12 months without interest, how much would the monthly payment be?

Solution

to. In this case:

\({a_{19}} = 2000 + 18\left( {550} \right)\)

\({a_{19}} = 2000 + 9900 = 11900\)

b. Between the numbers 2000 and 11900 we must find 11 arithmetic means, for which:

\(d = \frac{{11900 – 2000}}{{12}} = 825\)

5. Given the sequence \(7,\;22,\;45,\;76,115,162\) find the following 3 elements and the general expression of the element \(n\).

Solution

The sequence in question is not an arithmetic progression, since \(22 – 7 \ne 45 – 22\), but we can form a sequence with the differences of two consecutive elements and the following table shows the results:

Elements of the sequence \({b_n}\)	Sequence \(\;{c_n} = {b_n} – {b_{n – 1}}\)	\(d = {c_{n + 1}} – {c_n}\)
\({b_1} = 7\)	\({c_1} = {b_1}\)
\({b_2} = 22\)	\({c_2} = {b_2} – {b_1} = 15\)	\({c_2} – {c_1} = 8\)
\({b_3} = 45\)	\({c_3} = {b_3} – {b_2} = \)23	\({c_3} – {c_2} = 8\)
\({b_4} = 76\)	\({c_4} = {b_4} – {b_3} = 31\)	\({c_4} – {c_3} = 8\)
\({b_5} = 115\)	\({c_5} = {b_5} – {b_4} = 39\)	\({c_5} – {c_4} = 8\)
\({b_6} = 162\)	\({c_6} = {b_6} – {b_5} = 47\)	\({c_6} – {c_5} = 8\)

The third column of the above table tells us that the sequence \(15,\;23,31,39,\;47, \ldots .\); is an arithmetic sequence whose difference is \(d = 8\).

Next, we will write the elements of the sequence \({b_n}\) in terms of the sequence \({c_n},\)

\({b_1} = {c_1}\)

\({b_2} = {c_1} + {c_2}\)

\({b_3} = {b_2} + {c_3} = {c_1} + {c_2} + {c_3}\)

\({b_4} = {b_3} + {c_4} = {c_1} + {c_2} + {c_3} + {c_4}\)

In general you have:

\({b_n} = {c_1} + {c_2} + {c_3} + \ldots + {c_n}\;\)

When applying

\({S_n} = \frac{{n\left( {2{c_1} + \left( {n – 1} \right) d} \right)}}{2}\)

With \({c_1} = 7\) and \(d = 8,\) we obtain:

\({b_n} = \frac{{n\left( {14 + \left( {n – 1} \right) 8} \right)}}{2}\)

\({b_n} = n\left( {7 + 4\left( {n – 1} \right)} \right)\)

\({b_n} = n\left( {4n + 3} \right)\)

By applying the previous formula: \({b_7} = 217,\;{b_8} = 280,\;{b_9} = 351\)