Definition of Moment of Force (in Physics)

Evelyn Maitee Marin
Industrial Engineer, MSc in Physics, and EdD

The moment of force is a physical magnitude that expresses the effect of rotation around an axis, produced by a force acting on an object. This quantity, also known as torque/torque, and together with the calculation of the resultant force, is one of the fundamental parameters for the static analysis in the design of structures in engineering and architecture.

To better understand the effect associated with the moment of force, the unfortunate case where two vehicles collide at an intersection will be assumed. Intuitively, it is known that the effect of the impact force that vehicle 1 will produce on 2 (\({\vec F_{2/1}}\)) depends on the magnitude and direction of said force and its point of application (ignoring the effect of deformation and the friction). So for example, if the point of impact of 2 on 1 is in front of 1 (first diagram), it will rotate counterclockwise (from a top view). If it hits the rear of the vehicle, it will spin it clockwise (second diagram), and if the line of The action of the force of the impact passes through the center of gravity of the vehicle 1, it will produce translation (third diagram).

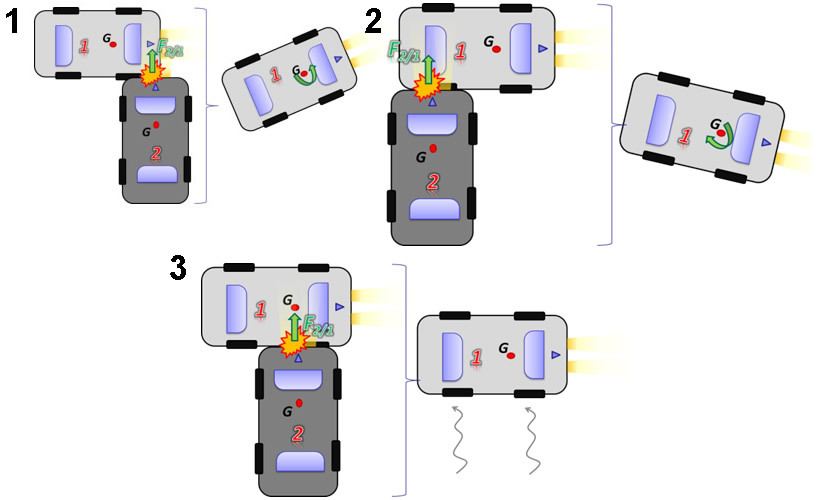
Considering the previous example, the moment of force (M) can be defined as a physical quantity which measures the tendency of a force to cause rotation of a rigid body about a fixed axis.

Now, since mention was made of rigid bodies in the formal definition, it is convenient to specify that this term is refers to a system of particles in which the closeness between them is such that the system is not deformed by the application of loads; that is to say, it is a body whose distance between any two points remains constant before the application of forces.

Moment of a force about a point

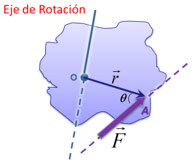If we consider a force \(\vec F\) that acts at a point A on a rigid body that has a fixed axis of rotation that passes through "o".

The Moment of the force with respect to the point "o" is defined as:

\(\overrightarrow {{M_o}} = \vec r \times \vec F\)

Where:

\(\vec r\): Position vector (goes from the reference point of the axis of rotation to the point of application of the force)

As can be seen, the moment of force with respect to a point is a vector quantity since it comes from a vector product, for this reason, it has magnitude, direction and sense. Each of these features is described below:

magnitude of M_either:

\( I \overrightarrow {{M_o}} I = I \vec r \times \vec F I \), this in turn can be expressed as:

Mo=r. F. sen

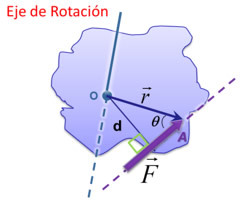As can be seen, the magnitude of the moment of a force about a point is influenced by the angle formed between the force (\(\vec F\)) and the position vector (\(\vec r\)). Well then:

If \(\vec r\;//\;\vec F \to \theta = 0^\circ \to {M_o} = r. F.{\rm{sin}}0^\circ \to {M_o} = 0\)

If \(\vec r\;\;\vec F \to \theta = 90^\circ \to {M_o} = r. F.{\rm{sin}}90^\circ \to {M_{oMAX}} = r. F\)

If d: Perpendicular distance between the reference point of the axis of rotation and the force (or its line of action), then:

d = r • sinθ ∴ Mo = F • d

In the international system the moment will have units of (N.m), in English (lb-f. ft), and so this quantity will have units of force per length.

Note: Since momentum is a quantity that is by definition vectorial, its units in the SI system are simply Newton.meters; In no case will it be expressed in Joules (J) which is equivalent to Newton.meter but associated with a scalar quantity such as work and energy.

Direction and Sense of M_either:

Since the vector \({\vec M_0}\) is calculated from a vector product, its direction must be perpendicular to the plane that contains \(\vec r\) and \(\vec F\), and its sense obeys the rule of the hand right.

It follows then that the moment of a force about a point is a vector quantity. Considering the axis of rotation, it follows that a force does not produce a moment in the following cases:

TO. If the force is parallel to the axis of rotation.

b. If the force (or its line of action) intersects the axis of rotation.

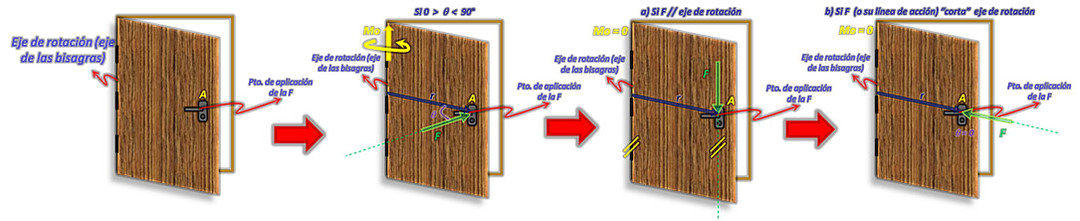
Moment of a force about an axis

The moment of a force about an axis is basically the projection of the moment of the force about an axis. It is therefore a scalar quantity whose sign indicates the direction of rotation of the rigid body around the axis and is determined with the following expression:

Where:

\({\vec M_{pto}}:\) is the moment of the force with respect to a point that belongs to the axis.

\(\widehat {axis}:\) is the unit vector of the axis.