Importance of the Cartesian Plane

He flat Cartesian has a fundamental characteristic and that is that, like any plane, it only has two dimensions: height and length, but it does not have depth. This is why the Cartesian plane is considered a two-dimensional system, because it precisely has two dimensions, as opposed to three-dimensional objects that have three dimensions (height, length, and width). depth).

The person who designed a Cartesian plane for the first time was René

A Cartesian plane is a two-dimensional system (by two-dimensional system is meant that which has two dimensions, for example, height and length, but not depth), where they are Cartesian coordinates, which correspond to a type of coordinates called orthogonal (by this term is called the general characteristic of perpendicularity). This Cartesian plane is constituted as a euclidean space, and where functions can be represented, from graphs, such as those used in geometry analytical or in physical. Within the Cartesian plane, the coordinates use axes called orthogonal as reference, and these axes intersect each other at a point of origin. In this way, the Cartesian coordinates respond and are defined according to the distance from the origin that the orthogonal projections have, according to the axes.

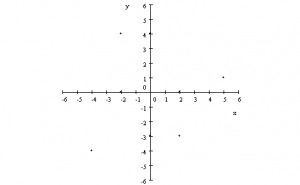
These plans are called Cartesians after the name of who first developed them: Rene Descartes. We said before that the Cartesian planes are two-dimensional systems and that the point where both intersect is called the zero point, or origin of the system. In the Cartesian plane, we will find two axes: one of them is located horizontally and is called "abscissa axis", assigning it the reference of the letter X. On the other hand, we find a vertical axis, called “axis of the ordinates”, and to which reference is given by the letter Y. By then cutting both lines, the Cartesian plane is divided into four regions, known as quadrants: the first quadrant (I) is located in the upper right region; the second quadrant (II) will be located in the upper left region; the third quadrant (III), we will find it located in the lower left region; while the four quadrant (IV), we will locate it in the lower right region. (As we can see in the image of this article).

Within this Cartesian plane that was formed for us, we can locate and assign a location within space to any point that can be located on said plane. To name a point, it is done by designating a “ordered pair”, for example: 4.5; will indicate that the point is at the intersection of +4 of the abscissa axis and +5 of the ordinate axis. These points are represented graphically from the perpendicular cut between the two lines that are drawn in the quadrants of the Cartesian plane that correspond in order to locate in space the point represented by the pair tidy.