Definition of Bernoulli's Principle/Equation

Bernoulli's Principle, often also called Bernoulli's Equation, is one of the most important concepts in hydrodynamics and fluid mechanics. It was formulated by the Swiss physicist and mathematician Daniel Bernoulli in 1738 as part of his work "hydrodynamics” and part of the conservation of energy in an ideal fluid in motion.

Let's imagine the following situation: We have a hose through which water is flowing, which leaves the hose with a certain velocity and a certain pressure. Then we proceed to partially cover the exit hole of the hose with a finger; by doing this we see how the water now comes out with greater speed. This is an example of Bernoulli's principle in action.

Ideal fluids in motion

Bernoulli's principle applies to ideal fluids in motion, so before going on to explain this principle, it is important to mention what we mean by ideal fluid. An ideal fluid is a simplification of a real fluid, this is done because the description of a fluid ideal is mathematically simpler and gives us useful results that can later be extended to the fluid case real.

There are four assumptions that are made to consider a fluid to be ideal and all of them have to do with flow:

• Steady flow: A steady flow is one in which the speed at which the fluid moves is the same at any point in space. In other words, we assume that the fluid does not undergo turbulence.

• Incompressibility: It is also assumed that an ideal fluid is incompressible, that is, that it has a constant density at all times.

• Non-viscosity: Viscosity is a property of fluids that, in general terms, represents the resistance that the fluid opposes to movement. Viscosity can be thought of as analogous to mechanical friction.

• Irrotational flow: With this assumption we refer to the fact that the moving fluid does not carry out any type of circular movement around any point of its path.

By making these assumptions and having an ideal fluid we greatly simplify the mathematical treatment and we also ensure the conservation of energy, which is the starting point towards the principle of Bernoulli.

Bernoulli's equation explained

Let us consider an ideal fluid moving through a pipe as shown in the following figure:

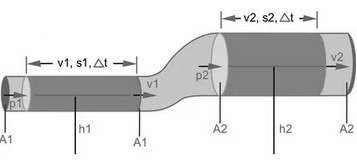
We will now use the Work and Kinetic Energy Theorem, which is another way of expressing the Law of Conservation of Energy, this tells us that:

\(W = {\rm{\Delta }}K\)

Where \(W\) is the total mechanical work and \({\rm{\Delta }}K\) is the change in kinetic energy between two points. In this system we have two types of mechanical work, one that is done by the force of gravity on the fluid and another that results from the pressure of the fluid. Let \({W_g}\) be the mechanical work done by gravity and \({W_p}\) be the mechanical work done by pressure, we can then say that:

\({W_g} + {W_p} = {\rm{\Delta }}K\)

Since gravity is a conservative force, the mechanical work done by it will be equal to the difference in gravitational potential energy between two points. The initial height at which the fluid is found is \({y_1}\) and the final height is \({y_2}\), therefore, we have:

\({W_g} = – {\rm{\Delta }}mg{\rm{\Delta }}y = – {\rm{\Delta }}mg\left( {{y_2} – {y_1}} \right )\)

Where \({\rm{\Delta }}m\) is the portion of mass of fluid that passes through a certain point and \(g\) is the acceleration due to gravity. Since the ideal fluid is incompressible, then \({\rm{\Delta }}m = \rho {\rm{\Delta }}V\). Where \(\rho \) is the density of the fluid and \({\rm{\Delta }}V\) is the portion of volume that flows through a point. Substituting this into the above equation we get:

\({W_g} = – \rho g{\rm{\Delta }}V\left( {{y_2} – {y_1}} \right)\)

Let us now consider the mechanical work done by the pressure of the fluid. Pressure is the force exerted per unit area, that is, \(F = PA\). On the other hand, mechanical work is defined as \(W = F{\rm{\Delta }}x\) where \(F\) is the applied force and \({\rm{\Delta }}x\) is the displacement carried out in this case on the x-axis. In this context we can think of \({\rm{\Delta }}x\) as the length of the portion of fluid that flows through a certain point. Combining both equations we have that \(W = PA{\rm{\Delta }}x\). We can realize that \(A{\rm{\Delta }}x = {\rm{\Delta }}V\), that is, it is the portion of volume that flows through that point. Therefore, we have that \(W = P{\rm{\Delta }}V\).

At the initial point, mechanical work is done on the system equal to \({P_1}{\rm{\Delta }}V\) and at the end point the system does mechanical work on the surroundings equal to \({P_2}{\rm{\Delta }}V\). The mechanical work due to the pressure of the fluid will then be the work done on the system minus the work it does on its surroundings, that is to say that:

\({W_p} = {P_1}{\rm{\Delta }}V – {P_2}{\rm{\Delta }}V = \left( {{P_1} – {P_2}} \right){\rm {\Delta }}V\)

Finally, the difference in kinetic energy \({\rm{\Delta }}K\) will be equal to the kinetic energy at the end point minus the kinetic energy at the start point. That is:

\({\rm{\Delta }}K = \frac{1}{2}{\rm{\Delta }}mv_2^2 – \frac{1}{2}{\rm{\Delta }}mv_1^ 2 = \frac{1}{2}{\rm{\Delta }}m\left( {v_2^2 – v_1^2} \right)\)

From the above, we know that \({\rm{\Delta }}m = \rho {\rm{\Delta }}V\). The above equation is then as:

\({\rm{\Delta }}K = \frac{1}{2}\rho {\rm{\Delta }}V\left( {v_2^2 – v_1^2} \right)\)

Substituting all the results obtained in the energy conservation equation, it is obtained that:

\(\left( {{P_1} – {P_2}} \right){\rm{\Delta }}V – \rho {\rm{\Delta }}V\left( {{y_2} – {y_1}} \right) = \frac{1}{2}\rho {\rm{\Delta }}V\left( {v_2^2 – v_1^2} \right)\)

We can factor the term \({\rm{\Delta }}V\) on both sides of the equation, this leads to:

\({P_1} – {P_2} – \rho g\left( {{y_2} – {y_1}} \right) = \frac{1}{2}\rho \left( {v_2^2 – v_1^2 } \right)\)

Developing the missing products we have to:

\({P_1} – {P_2} – \rho g{y_2} + \rho g{y_1} = \frac{1}{2}\rho v_2^2 – \frac{1}{2}\rho v_1^ 2\)

Rearranging all the terms on both sides of the equation we obtain that:

\({P_1} + \rho g{y_1} + \frac{1}{2}\rho v_1^2 = {P_2} + \rho g{y_2} + \frac{1}{2}\rho v_2^ 2\)

This equation is a relationship between the initial state and the final state of our system. We can finally say that:

\(P + \rho gy + \frac{1}{2}\rho {v^2} = constant\)

This last equation is Bernoulli's Equation from which the principle of it is derived. Bernoulli's Principle is a conservation law for an ideal fluid in motion.

References

David Halliday, Robert Resnick & Jearl Walker. (2011). Fundamentals of Physics. United States: John Wiley & Sons, Inc.