Definition of Aphelion and Perihelion

Angel Zamora Ramirez
Degree in physics

Aphelion and perihelion are two points that belong to the orbit of a planet around the Sun. The aphelion is the point that corresponds to the maximum distance that the planet reaches with respect to the Sun. On the contrary, perihelion, also called perigee, is the point at which said planet is at a minimum distance from the Sun.

The orbits that the planets trace in their translational movement are elliptical and the Sun is located at one of the focuses of the ellipse. This peculiarity of planetary movement means that the distance between a planet and the Sun is not always the same. There are two points at which a planet in its path around the Sun is at a distance maximum and at a minimum distance from it, these points are known as “aphelion” and “perihelion”, respectively.

Kepler's First Law: Orbits are elliptical

Around the 16th century, one of the great revolutions in the history of science occurred and it was the publication of Copernicus's heliocentric model. Nicolás Copernicus was a Polish mathematician and astronomer who, after years of study and research in Mathematical Astronomy concluded that the Earth and the rest of the planets moved along circular paths around the Sun.

This heliocentric model of Copernicus not only challenged the geocentric model of Ptolemy and centuries of observations and measurements, but also challenged an anthropocentric tradition established by the church Catholic. The latter made Copernicus affirm that his model was only a strategy to better determine precision the position of the stars in the celestial vault but that it was not a representation of the reality. Despite this, the evidence was clear and his heliocentric model led to a Copernican revolution that changed astronomy forever.

During that same century, the Danish astronomer Tycho Brahe made very precise measurements of the position of the planets and other celestial bodies. During his career, Tycho Brahe invited the German mathematician Johannes Kepler to work with him on his research, which was accepted by Kepler. Brahe was overzealous with the data he had collected, so Kepler's access to it was very limited. Furthermore, Brahe treated Kepler as his subordinate, which the latter did not like at all and the relationship between them was complicated.

After Tycho Brahe's death in 1601, Kepler took possession of his precious data and observations before they were claimed by his heirs. Kepler was aware that Brahe lacked the analytical and mathematical tools to understand planetary motion from his observations. Thus, Kepler's meticulous study of Brahe's data answered several questions regarding planetary motion.

Kepler was totally convinced that Copernicus's heliocentric model was correct, however, There were some discrepancies with the apparent position that the planets had in the celestial vault throughout the year. After carefully analyzing the data collected by Brahe, Kepler realized that the observations best fit a heliocentric model in which the planets trace elliptical orbits around the Sun, and not circular orbits as he proposed Copernicus. This is known as “Kepler's First Law” and was published along with Kepler's Second Law in 1609 in his work “Astronomía Nova”.

To better understand this we have to first understand the definition and structure of an ellipse. An ellipse is defined as a closed curve whose points that form it satisfy that the sum of the distances between these and other points called “foci” is always the same. Let's consider the following ellipse:

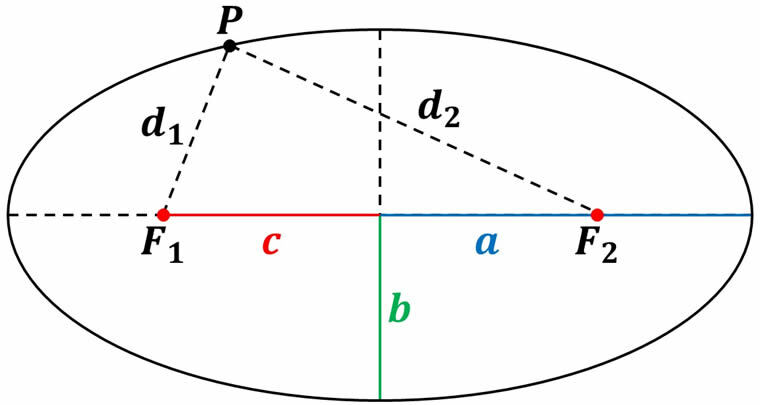
In this ellipse the points \({F_1}\) and \({F_2}\) are the so-called “foci”. An ellipse has two axes of symmetry that are perpendicular to each other and that intersect at its center. The length \(a\) is called the “semimajor axis” and corresponds to the distance between the center of the ellipse and its extreme point, which is along the major axis of symmetry. Likewise, the length \(b\) known as the “semi-minor axis” is the distance between the center of the ellipse and its extreme point located along the minor axis of symmetry. The distance \(c\) that exists between the center of the ellipse and any of its foci is known as “focal semidistance”.

By its own definition, if we take any point \(P\) that belongs to the ellipse and plot the distance \({d_1}\) between the point \(P\) and the focus \({F_1}\), and another distance \({d_2}\) between the point \(P\) and the other focus \({F_2}\), these two distances satisfy:

\({d_1} + {d_2} = 2a\)

Which is valid for any point on the ellipse. Another magnitude that we can mention is the “eccentricity” of the ellipse which is denoted by the letter \(\varepsilon \) and determines how oblate the ellipse is. The eccentricity is given by:

\(\varepsilon = \frac{c}{a}\;;\;0 \le \varepsilon \le 1\)

With all this in our hands, we can now talk about the elliptical orbits of the planets around the Sun. A somewhat exaggerated diagram of the orbit of a planet around the Sun would be the following:

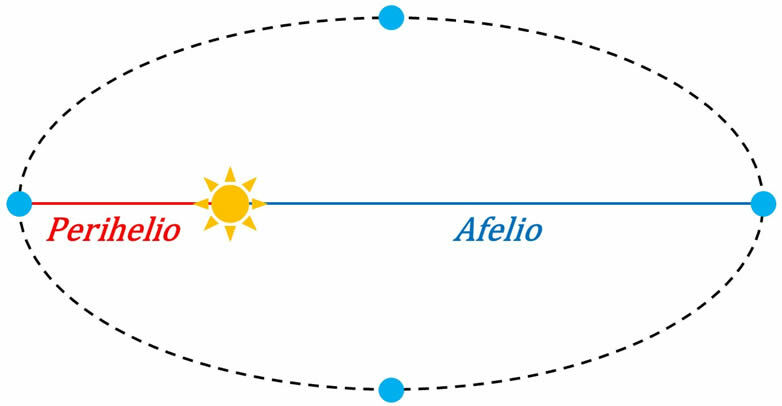
In this diagram we can realize that the Sun is at one of the focuses of the planet's elliptical orbit. The perihelion (\({P_h}\)) will be the distance given by:

\({P_h} = a – c\)

On the other hand, the aphelion (\({A_f}\)) will be the distance:

\({A_f} = a + c\)

Or, both distances in terms of the eccentricity of the orbit will be:

\({P_h} = \left( {1 – \varepsilon } \right) a\)

\({A_f} = \left( {1 + \varepsilon } \right) a\)

Planetary orbits, at least in our Solar System, have a very small eccentricity. For example, the Earth's orbit has an approximate eccentricity of \(\varepsilon \approx 0.017\). The semimajor axis of the Earth's orbit is about \(a \approx 1.5 \times {10^8}\;km\). With everything mentioned above we can calculate that the perihelion and aphelion of the Earth will be: \({P_h} \approx 1.475 \times {10^8}\;km\) and \({A_f} \approx 1.525 \times { 10^8}\;km\).