Example of Sum of Fractions with Different Denominator

Fractions are made up of two main parts: a denominator and a numerator. The denominator tells us what are we talking about, if of means, thirds, quarters, etc., and it goes below the fraction line. The numerator indicates how manythere are of those halves, thirds, fourths, etc., and goes above the fraction line.

In arithmetic operations, such as addition, there is a general requirement: that all fractions have the same denominator to add to each other directly. Here the question arises: What do we do when we have different denominators in a problem, and we want to add the fractions?

To solve a case of adding fractions with different denominators, a series of well-defined steps must be followed:

• Find the common denominator for all fractions
• Convert the fractions to the common denominator
• Add together all converted numerators
• Present the result as a mixed or improper fraction

An example will be solved below, with the explanation of each step.

Example of adding fractions with different denominators

There are five fractions that must be added:

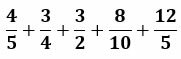
Find the common denominator for all fractions

Looking at the fractions of the problem, we find in total four different denominators: 2, 4, 5, 10. To find a common denominator, we can multiply between these denominators:

• 2*4 = 8. The number 8 is not a multiple of 5 or 10. You have to try again.
• 2*5 = 10. The number 10 is not a multiple of 4. You have to try again.
• 2*10 = 20. The number 20 is a multiple of 2, 4, 5 and 10 at the same time.

The common denominator for 2, 4, 5, and 10 is the number 20.

Convert the fractions to the common denominator

To transform the original fractions to fractions with the common denominator, you have to multiply. Each fraction by the multiple it fits. For example: 4/5 must be multiplied by 4, so that the denominator 5 becomes 20, and the numerator 4 also fits.

The latter are the fractions that we are going to work with now.

Add together all converted numerators

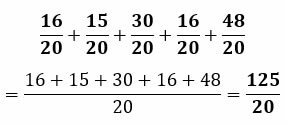
Present the result as a mixed or improper fraction

The result is an improper fraction that can also be presented as a mixed fraction, until it is simplified to a smaller denominator:

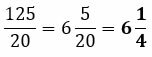
Now you know how to correctly solve a sum of fractions with different denominators.

You may also like:

• Sum of fractions
• Sum of mixed fractions
• Sum of fractions with integers
• Subtraction of fractions
• Multiplication of fractions
• Division of fractions
• Square root of fractions