Algebraic Subtraction Example

Algebraic subtraction is one of the fundamental operations in the study of algebra. It is used to subtract monomials and polynomials. With algebraic subtraction we subtract the value of one algebraic expression from another. Because they are expressions that are composed of numerical terms, literals, and exponents, we must be attentive to the following rules:

Subtraction of monomials:

Subtracting two monomials can result in a monomial or a polynomial.

When the factors are equal, for example, the subtraction 2x - 4x, the result will be a monomial, since the literal is the same and has the same degree (in this case, 1, that is, without an exponent). We will only subtract the numerical terms, since, in both cases, it is the same as multiplying by x:

2x - 4x = (2 - 4) x = –2x

When the expressions have different signs, the sign of the factor that we subtract will change, applying the law of signs: when subtracting an expression, if it has a negative sign, it will change to positive, and if it has a positive sign, it will change to negative. To avoid confusion, we write the numbers with a negative sign, or even all expressions, in parentheses: (4x) - (–2x) .:

(4x) - (–2x) = 4x + 2x = 6x.

We must also remember that in subtraction, the order of the factors must be taken into account:

(4x) - (–2x) = 4x + 2x = 6x.
(–2x) - (4x) = –2x - 4x = –6x.

In the case that the monomials have different literals, or in the case of having the same literal, but with different degree (exponent), then the result of the algebraic subtraction is a polynomial, formed by the minuend, minus the subtracting. To distinguish the subtraction from its result, we write minuend and subtrahend in parentheses:

(4x) - (3y) = 4x - 3y
(a) - (2a²) - (3b) = a - 2a² - 3b
(3m) - (–6n) = 3m + 6n

When there are two or more common terms in the subtraction, that is, with the same literals and of the same degree, they are subtracted from each other, and the subtraction is written with the other terms:

(2a) - (–6b²) - (–3a²) - (–4b²) - (7a) - (9a²) = [(2a) - (7a)] - [(–3a²) - (9a²)] - [(–6b²) - (–4b²)] = [–5a] - [–10b²] - [–6a²] = –5a + 12a² + 2b²

Subtraction of polynomials:

A polynomial is an algebraic expression that is made up of additions and subtractions of the terms with different literals and exponents that make up the polynomial. To subtract two polynomials, we can follow the following steps:

We will subtract c + 6b² –3a + 5b of 3a² + 4a + 6b –5c - 8b²

1. We order the polynomials in relation to their letters and their degrees, respecting the sign of each term:

 4th + 3rd² + 6b - 8b²
 –3a + 5b + 6b² + c

1. We group the subtractions of the common terms, in the minuend – subtrahend order: [(4a) - (- 3a)] + 3a² + [(6b) - (5b)] + [(- 8b²) - (6b²)] - c
2. We carry out the subtractions of the common terms that we put between parentheses or brackets. Let us remember that when being subtracted, the terms of the subtrahend change sign: [4a + 3a] + 3a² + [6b - 5b] + [- 8b² - 6b²] - c = 7a + 3a² + b - 14b² - c

To better understand the change of signs in the subtraction, we can do it vertically, placing the minuend at the top, and the subtrahend at the bottom:

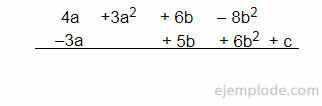
As we are doing a subtraction, the signs of the subtrahend will change, so if we express it as a sum in which all the signs of the subtrahend are reversed, then it will remain like this and we resolve:

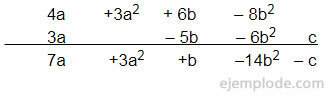
Subtraction of monomials and polynomials:

As we can deduce from what has already been explained, to subtract a monomial from a polynomial, we will follow the revised rules. If there are common terms, the monomial will be subtracted from the term; If there are no common terms, the monomial is added to the polynomial as the subtraction of one more term:

If we have (2x + 3x² - 4y) - (–4x²) We align the common terms and do the subtraction:

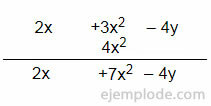
(Remember that subtracting a negative number is equivalent to adding it, that is, its sign is reversed)

If we have (m - 2n² + 3p) - (4n), we perform the subtraction, aligning the terms:

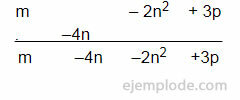
It is advisable to order the terms of a polynomial, to facilitate their identification and the calculations of each operation.

• It may interest you: Algebraic sum

Examples of algebraic subtraction

(3x) - (4x) = –x
(–3x) - (4x) = –7x
(3x) - (–4x) = 7x
(–3x) - (–4x) = x
(2x) - (2x²) = 2x - 2x²
(–2x) - (2x²) = –2x - 2x²
(2x) - (–2x²) = 2x + 2x²
(–2x) - (–2x²) = –2x + 2x²
(–3m) - (4m²) - (4n) = –3m - 4m² - 4n
(–3m) - (–4m²) + (4n) = –3m + 4m² + 4n
(–3m) + (4m²) - (–4n) = –3m - 4m² + 4n
(3m) - (4m²) - (4n) = 3m - 4m² - 4n
(2b² + 4c + 3a³) - (5a + 3b + c²) = - 5th + 3rd³ - 3b + 2b² + 4c - c²
(–2b² + 4c + 3a³) - (5a + 3b - c²) = - 5th + 3rd³ - 3b - 2b² + 4c + c²
(2b² + 4c - 3a³) - (5a + 3b - c²) = - 5th - 3rd³ - 3b + 2b² + 4c + c²
(2b² - 4c + 3a³) - (5a + 3b + c²) = - 5th + 3rd³ - 3b + 2b² - 4c - c²
(2b² + 4c + 3a³) - (–5a + 3b + c²) = 5th + 3rd³ - 3b + 2b² + 4c - c²
(–2b² - 4c - 3a³) - (–5a - 3b - c²) = 5th - 3rd³ + 3b - 2b² - 4c + c²
(4x² + 6y + 3y²) - (x + 3 x² + and²) = - x + x² + 6y + 2y²
(–4x² + 6y + 3y²) - (x + 3 x² + and²) = - x - 7x² + 6y + 2y²
(4x² + 6y + 3y²) - (x - 3 x² + and²) = - x + 7x² + 6y + 2y²
(4x² - 6y - 3y²) - (x + 3 x² + and²) = - x + x² - 6y - 4y²
(4x² + 6y + 3y²) - (–x + 3 x² - Y²) = x + x² + 6y + 4y²
(–4x² - 6y - 3y²) - (–x - 3 x² - Y²) = x –x² - 6y - 2y²
(x + y + 2z²) - (x + y + z²) = z²
(x + y + 2z²) - (–x + y + z²) = 2x + z²
(x - y + 2z²) - (–x + y + z²) = 2x - 2y + z²
(x - y - 2z²) - (x + y + z²) = 2y - 3z²
(–X + y + 2z²) - (x + y - z²) = –2x + 3z²
(–X - y - 2z²) - (-X and Z²) = - z²

Follow with:

• Algebraic sum