Distributive Property Example

The distributive property is a property of multiplication that tells us that if we multiply one number by another, the result is the same as if we multiply the first number by the addition or subtraction that results in the second number.

To express a multiplication with a distributive property, we use the parentheses.

For example, if we have the multiplication:

6 X 9 = 54

We know that the number 9 is the result of adding 5 + 4. Applying the distributive property, the multiplication will be expressed like this:

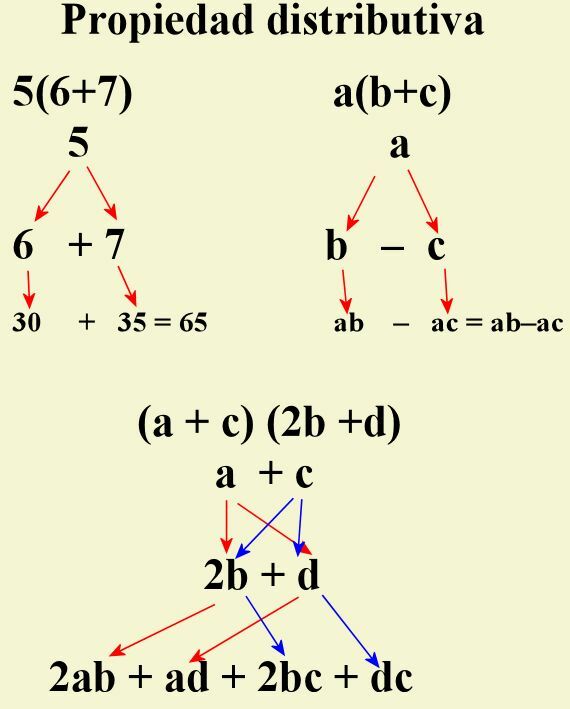
6(5+4)

This means that we will multiply the number 6 by each of the members of the sum, and then we will perform the sum:

6 (5 + 4) = (6X5) + (6X4) = 30 + 24 = 54

And how we see, we get the same result. The distributive property also applies to subtraction:

6 (10–1) = (6X10) - (6X1) = 60 - 6 = 54

This distributive property is also used to obtain the product of two additions or subtractions, or of an addition and a subtraction. In these cases, each of the members of the first operation is multiplied by each of the members of the second operation, and then the operations are performed:

(5 + 2) (3 + 4) = (5X3) + (5X4) + (2X3) + (2X4) = 15 + 20 + 6 + 8 = 49

Performing the operations of the parentheses first: 7 X 7 = 49

(7–3) (6–2) = (7X6) + (7X – 2) + (- 3X6) + (- 3X – 2) = 42–14–18 + 6 = 16

Performing the operations of the parentheses first: 4 X 4 = 16

The distributive property is useful especially for calculating very large numbers, as well as in algebra.

If we have a complex number, such as 5648, and we want to multiply it by 8, we can decompose 5648 into decimal notation, multiply the components by 8, and then do the addition:

8 (5000 + 600 + 40 + 8) = (8X5000) + (8X600) + (8X40) + (8X8) = 40000 + 4800 + 320 + 16 = 45136.

In algebra many numerical values ​​are replaced by literal values ​​(expressed with letters), as well as values ​​with exponents, and here the distributive property is very useful. The same rules that we already explained are followed:

(a + 3ab + c) (b – 2) = (ab) + (- 2a) + (3ab²) + (- 6ab) + (bc) + (- 2c) = [We order and reduce the signs] –2a + ab – 6ab + 3ab²+ bc – 2c = –2a – 5ab + 3ab²+ bc – 2c [note that we reduced the common terms that the literal ab has]

Examples of distributive property:

Sergio has 7 piggy banks, and in each one of them he has deposited the same amount of coins and bills. In each one he has put 3 bills of 10 pesos, and 4 coins of 5 pesos. That means that in each piggy bank he has put 30 pesos in bills, and 20 pesos in coins. To calculate how much money you have saved in total in your piggy banks, perform the following calculation:

(30 + 20) 7 = (30X7) + (20X7) = 210 + 140 = 350

That is, he first multiplied the total of money that he put in bills by the total of piggy banks, and he then he multiplied the total of the money in coins by the total of piggy banks, and then added the results.

His brother Esteban does the calculation by adding the total of what he put in each piggy bank and then multiplying it by the total of piggy banks:

30 pesos in bills of 10, and 20 pesos in coins of 5: 30 + 20 = 50

We multiply the total of each piggy bank by the total of piggy banks: 50 X 7 = 350

As we can see, they both reached the same result.

• (4 + 2) 3 = (4 x 3) + (2 x 3) = 12 + 6 = 18
• (6 + 9) 10 = (6 x 10) + (9 x 10) = 60 + 90 = 150
• 5x (3 - 4) = ((5 x) (3)) + ((5x) (- 4)) = 15x - 20x = –5x
• (3 + 9) 9 = (3 X 9) + (9 X 9) = 27 + 81 = 108
• 2 (5 + 7) = (2 X 5) + (2 X 7) = 24
• (8 + 5) (5 + 7) = (8X5) + (8X7) + (5X5) + (5X7) = 40 + 56 + 25 + 35 = 156
• (11–3) (8–3) = (11X8) + (11X – 3) + (- 3X8) + (- 3X – 3) = 88–33–24 + 9 = 40
• (a + 2b + c) 3 = (3a) + (6b) + (3c) = 3rd + 6b + 3c
• (a + b) (a – b) = [(a) (a)] + [(a) (- b)] + [(b) (a)] + [(b) (- b)] = [ to²] + [- ab] + [ab] + [- b²] = a²–B²
• (a – b – c) (a²+ 3ab + 4b²+ c) = (a³) + (3rd²b) + (4ab²) + (ac) + (–a²b) + (–3ab²) + (–4b³) + (–Bc) + (–a²c) + (–3abc) + (–4 b²c) + (–c²) = a³ + 3a²b + 4ab² + ac - a²b - 3ab² - 4b³ - bc - a²c - 3abc - 4b²c - c² = a³ + 2a²b + ab² - 4b³ + ac - bc - 3abc - a²c - 4b²c - c²

If we add two numbers and then multiply the result by another number, we obtain the same result that if we multiply each of the addends by the same number and then add the products obtained.
Examples of distributive property:
Sergio counts all the money that he kept in his piggy banks and performs the following calculation:
(30 + 20) x 7 = 350
He added the value of three bills (30) and two coins (20), and multiplied the result by 7.
20 x 7 + 30 x 7 = 140 + 210 = 350
In this case he multiplied the value of the coins (20) by seven and multiplied the value of the bills (30), and added both results. He concluded that in both situations the end result is the same.
In the distributive property the product of a sum or addition by a number is equal to the sum of the products of each of the addends by the same number.
Other examples of the distributive property:
1) (4 + 2) x 3 = 4 x 3 + 2 x 3 = 18
2) (6 + 9) x 10 = 6 x 10 + 9 x 10 = 150
3) 5 x (3 + 4) = 5 x 3 + 5 x 4 = 35
4) (3 + 9) x 9 = 3 x 9 + 9 x 9 = 108
5) 2 x (5 + 7) = 2 x 5 + 2 x 7 = 24
Keep in mind that in the distributive property the (+) and (-) signs separate the terms. And the operations that are inside the parentheses are solved first.