Real Numbers Example

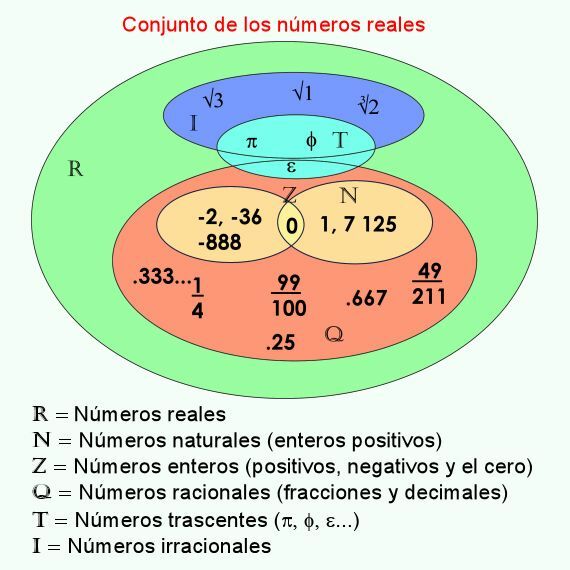
The real numbers They are the set of numbers on which they study mathematics, since they are all the numbers that can be represented on a number line. As a set, the real numbers contain the following subsets:

The whole numbers (Z), which in turn is composed of:

The natural numbers (N): They are all positive integers.
Negative numbers.
The zero.

Rational numbers (Q), which are all those that are represented by a quotient or fraction, or by exact or periodic decimal numbers. They are divided into:

Fractions, which express the quotient between two quantities.
Decimals, which express the result of a fractional quotient.

Irrational numbers (I), They are those that express numerical results whose decimal result is not periodic and extends to infinity.

The Transcendent numbers (T), are a subset of the irrational numbers and some rational numbers, which express very important mathematical relationships, such as the relationship between the circumference and the radius, the number pi (π).

Generally, the set of real numbers is represented by the letter "R", and the operations and different properties of operation studied in arithmetic and algebra are applied to them:

• Sum.
• Subtraction.
• Multiplication.
• Division.
• Empowerment
• Root.
• Associative Property.
• Commutative Property.
• Distributive property.
• Lock property.
• Neutral element.

Click on the image to see it bigger

Real numbers can be defined as the set of all numbers with which we usually perform mathematical operations in arithmetic and algebra. A Real numbers are contrasted with imaginary numbers, which are all those that cannot be represented in a number line, and corresponding to the product b * i, where b is a real number, and the constant i represents the square root of -1.

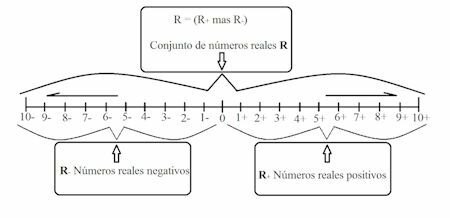
The real numbers together are represented by the letter R but there is a subdivision that contains the following two:

1. Positive real numbers = R+
2. Negative real numbers = R-

Representing R + to the positive real numbers, which on the number line correspond to the positive and which are generally to the right.
Representing R- to negative numbers, which on the number line correspond to the negative and are generally to the left.

Example of real numbers:

Natural numbers (positive integers):

1
3
7
9
15
45
678
987
3456
2345
234567
384512
95732486
654821958
2468957888

Negative integers:

 – 1
– 3
– 7
– 9
– 15
– 45
– 678
– 987
– 3456
– 2345
– 234567
– 384512
– 95732486
– 654821958
– 2468957888

Zero: 0

Rational numbers:

Fractional numbers:

½
– ¼
14/35
2/7
5/9
2/3
– 4/7
6/9
9/15
45/99
65/85
– 77/88
12/101
1/125
4/222

Decimal numbers:

.25
0.999,
0.625
0.3333333….
0.1234512345…
0.625
0.11111
0.512
0.99
0.000001
0.0000000002
0.15348
0.000000000000000024
0.000100040002
0.5248

Transcendental Numbers:

π = 3.14159265358979323846… (pi);
φ = 1.618033988749894848204586834365638117720309… (fi or golden number)
ε = 2.7182818284590452353602874713527… (Euler number)

Irrational numbers:

√5
√2
√3
³√3
⁵√2
√7
√11
√101
⁴√99
⁷√12
³√9
⁵√33
⁷√2
⁴√4
³√122