Quadratic Function Example

The quadratic function expresses the relationship that solves a quadratic equation. The name of quadratic is because it always has a term squared. By forming a table with the values ​​that the variables x and y can take, and representing the values ​​in the Cartesian plane, the result is a curved line called a parabola.

Equations of the second degree have the form y = ax² + bx + c. In this equation, the value of y will depend on the value that x takes.

To solve this equation, the value of x must be found that results in the value of y being equal to 0, so the equation must be formulated as:

ax² + bx + c = 0

To do this, we must balance the equation such that the result is 0:

4x² + 3x –5 = 6 >>> (We subtract 6 from both sides) >>> 4x² + 3x –5 –6 = 6 –6 >>> 4x² + 3x –11 = 0

2x² + 6 = 4x –4 >>> (We subtract 4x – 4 from both sides) >>> (2x² + 6) - (4x – 4) = (4x – 4) - (4x – 4) >>> 2x² - 4x +10 = 0

Once we have the equation of the form ax² + bx + c = 0, we solve it with the equation to solve the equations of the second degree. This equation allows us to obtain the values ​​of x with which the equation is solved.

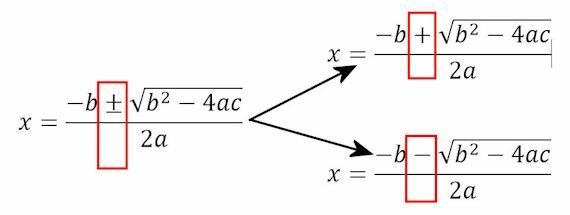
These solution values ​​will coincide with the 0 point on the x-axis, and will be the solution values ​​of the equation. The values ​​between these points may indicate some of the values ​​in the parabola.

In their practical application, these second degree functions are used in physics to calculate the parabolic throw of a projectile, the distance traveled, the total distance, the time and the maximum height and represent them graphically. It also has applications in economics, statistics, sports, and medicine.

Once the limit values ​​are located, we can make a table of the function, substituting the values ​​of x, and we can graph the values ​​obtained.

Examples of quadratic functions:

Example 1

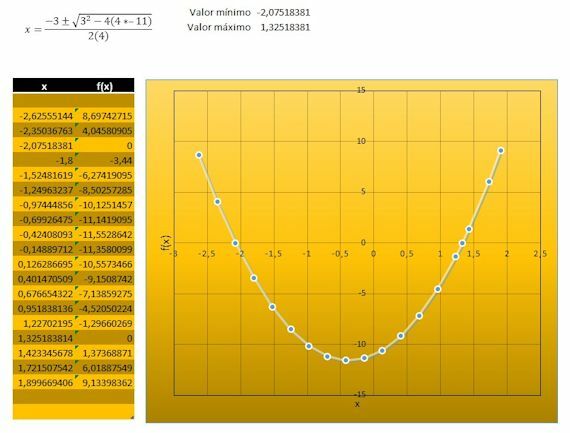
Calculate the function, table, and graph for equation 4x² + 3x –5 = 6

We start by making the result of the equation equal to zero:

We subtract 6 from both sides: 4x² + 3x –5 –6 = 6 –6

We get 4x² + 3x –11 = 0

We resolve:

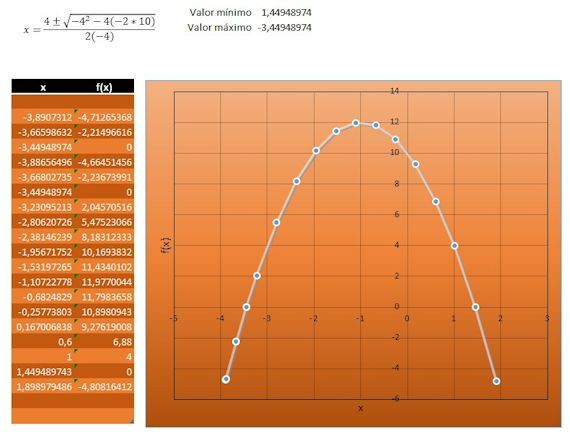
Example 2

Calculate the function, table, and graph for the equation –2x² + 6 = 4x –4

We start by making the result of the equation equal to zero:

We subtract 4 from both sides: (–2x² + 6) - (4x – 4) = (4x – 4) - (4x – 4)

We get –2x² - 4x +10 = 0

We resolve:

Example 3

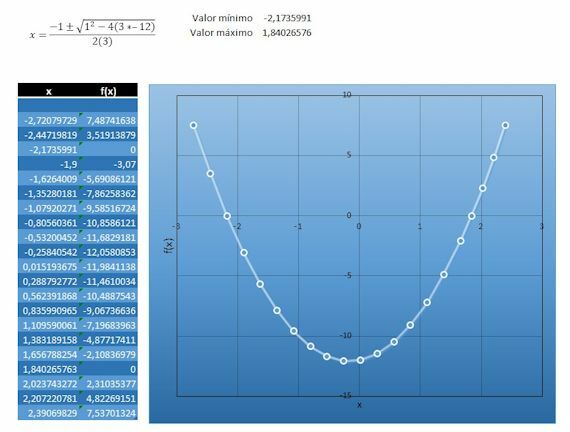
Calculate the function, table, and graph for equation 3x² –12 = –x

We start by making the result of the equation equal to zero:

We add x to both sides: 3x² - 12 + x = - x + x

We get 3x² + x –12 = 0

We resolve: