Example of Addition of Mixed Fractions

The mixed fractions are those formed by a whole part and one part of proper fraction (that does not complete an integer). They represent values ​​that exceed unity and that are still accompanied by another small portion. These values ​​also participate in arithmetic operations such as addition, which has a simple four-step method of solving:

• Convert mixed fractions to improper fractions
• Find the common denominator of all
• Add the numerators with each other, with the same denominator
• Convert improper result to mixed fraction

Each of the steps to be followed is explained with an example.

Example of adding mixed fractions

We have three mixed fractions that must be added:

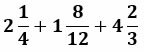
From them, the steps will be followed in detail.

Convert mixed fractions to improper fractions

Here we change the integer part for a fraction expression, and add it to the proper part:

The mixed fractions have been transformed, and we will continue working with:

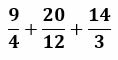
Find the common denominator of all

Fractions that have different denominators cannot be added as they are, because it is different to speak of fourths, than of twelfths and thirds. To add them, you have to find the common denominator of all.

We can first multiply the smallest denominators.

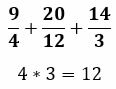
Common denominator = 12

The result, 12, will be a suitable denominator for the first and last fractions. It is also the same as the 12 denominator in the other fraction, so look no further. 12 is the common denominator for all of them.

Add the numerators to each other, with the same denominator

We already have the common denominator. Now you have to convert the fractions to that denominator:

• In the first fraction, you have to multiply everything by 3, so that the fourths become twelfths.
• In the second fraction, you don't have to do anything. There are already twelfths.
• In the third fraction, you have to multiply everything by 4, so that the thirds become twelfths.

These fractions of denominator 12 have to be added directly, accumulating their numerators:

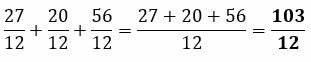
Convert improper result to mixed fraction

To get the result in mixed fraction mode, divide the numerator by the denominator. In other words, the 103 will be distributed in packages of 12. We will see at the end how many twelfths are left:

In this way, there are 8 integers and a proper part of 7 twelfths, which are represented:

Now you know how to correctly solve a sum of mixed fractions.

You may also like:

• Sum of fractions
• Subtraction of fractions
• Sum of fractions with integers
• Sum of fractions with different denominators
• Multiplication of fractions
• Division of fractions
• Square root of fractions