Example of binomial squared

A binomial is an algebraic expression that consists of two terms that are added or subtracted. In turn, these terms can be positive or negative.

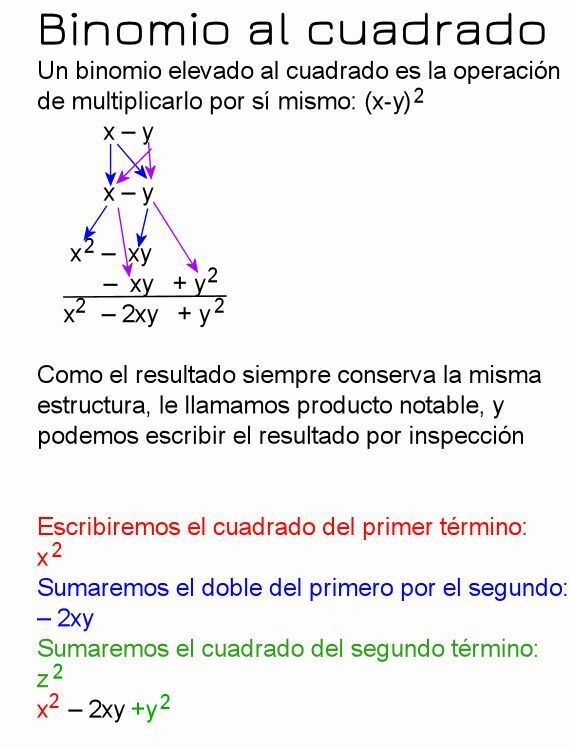
A binomial squared is a algebraic sum that adds by itself, that is, if we have the binomial a + b, the square of that binomial is (a + b) (a + b) and it is expressed as (a + b)².

The product of a squared binomial is called a perfect square trinomial. It is called a perfect square, because the result of its square root is always a binomial.

As in all algebraic multiplication, the result is obtained by multiplying each of the terms of the first term, by the terms of the second, and adding the common terms:

When squaring the binomial: x + z, we will do the multiplication as follows:

(x + z)² = (x + z) (x + z) = (x) (x) + (x) (z) + (z) (x) + (z) (z) = x²+ xz + xz + z² = x²+ 2xz + z²

If the binomial is x – z, then the operation will be:

(x – z)² = (x – z) (x – z) = (x) (x) + (x) (–z) + (–z) (x) + (z) (z) = x²–Xz – xz + z² = x²–2xz + z²

Here, it is convenient to remember some important points:

Every number squared always gives a positive number as a result: (a) (a) = a²; (–A) (–a) = a²

Every exponent raised to a power is multiplied by the power to which it is raised. In this case, all exponents squared are multiplied by 2: (a³)² = a⁶; (–B⁴)² = b⁸

The result of a squared binomial is always a perfect square trinomial. These types of operations are called notable products. In remarkable products, the result can be obtained by inspection, that is, without doing all the operations in the equation. In the case of the squared binomial, the result is obtained with the following inspection rules:

1. We will write the square of the first term.
2. We will add twice the first for the second term.
3. We will add the square of the second term.

If we apply these rules to the examples we used above, we will have:

(x + z)²

1. We will write the square of the first term: x²
2. We will add twice the first by the second term: 2xz
3. We will add the square of the second term: z².

The result is: x²+ 2xz + z²

(x – z)²

1. We will write the square of the first term: x².
2. We will add twice the first by the second term: –2xz.
3. We will add the square of the second term: z².

The result is x²+ (- 2xz) + z² = x²–2xz + z²

As we can see, in the case that the operation of multiplying the first by the second term is a negative result, it is the same as directly subtracting the result. Remember that adding a negative number, and reducing the signs, the result will be subtracting the number.

Examples of binomials squared:

 (4x³ - 2 and²)²

The square of the first term: (4x³)² = 16x⁶
The double product of the first and the second: 2 [(4x³)(-2 and²)] = –16x³Y²
The square of the second term: (2y²)² = 4y⁴
(4x³ - 2 and²)² = 16x⁶ –16x³Y²+ 4y⁴
(5th³x⁴ - 3b⁶Y²)² = 25a⁶x⁸ - 30th³b⁶x⁴Y²+ 9b¹²Y⁴
(5th³x⁴ + 3b⁶Y²)² = 25a⁶x⁸ + 30a³b⁶x⁴Y²+ 9b¹²Y⁴
(- 5th³x⁴ - 3b⁶Y²)² = 25a⁶x⁸ + 30a³b⁶x⁴Y²+ 9b¹²Y⁴
(- 5th³x⁴ + 3b⁶Y²)² = 25a⁶x⁸ - 30th³b⁶x⁴Y²+ 9b¹²Y⁴
(6mx + 4ny)² = 36m²n² + 48mnxy + 16n²Y²
(6mx - 4ny)² = 36m²n² - 48mnxy + 16n²Y²
(–6mx + 4ny)² = 36m²n² - 48mnxy + 16n²Y²
(–6mx - 4ny)² = 36m²n² + 48mnxy + 16n²Y²
(4vt - 2ab)² = 16v²t² - 16abvt + 4a²b²
(–4vt + 2ab)² = 16v²t² - 16abvt + 4a²b²
(–4vt - 2ab)² = 16v²t² + 16abvt + 4a²b²
(4vt + 2ab)² = 16v²t² + 16abvt + 4a²b²
(3x⁵ + 8)² = 9x¹⁰ + 48x⁵ + 64
(- 3x⁵ – 8)² = 9x¹⁰ + 48x⁵ + 64
(- 3x⁵ + 8)² = 9x¹⁰ - 48x⁵ + 64
(3x⁵ – 8)² = 9x¹⁰ - 48x⁵ + 64
(3rd³b - 3ab³)² = 9a⁶b² - 18⁴b⁴ + 9a²b⁶
(3rd³b + 3ab³)² = 9a⁶b² + 18a⁴b⁴ + 9a²b⁶
(- 3rd³b - 3ab³)² = 9a⁶b² + 18a⁴b⁴ + 9a²b⁶
(–3a³b + 3ab³)² = 9a⁶b² - 18⁴b⁴ + 9a²b⁶
(2a - 3b²)² = 4a² + 12 ab² + 9b⁴
(2a + 3b²)² = 4a² + 12 ab² + 9b⁴
(–2a + 3b²)² = 4a² - 12 ap² + 9b⁴
(2a - 3b²)² = 4a² - 12 ap² + 9b⁴