Characteristics of Triangles

A Triangle is a three-sided polygon. This is the fundamental polygon, which can be considered as component of all other superiors, which are the square, the pentagon, the hexagon, and all of the following.

The characteristics of the Triangles are:

As a geometric figure, it has its sides joined at points called vertices. Therefore, it will have three vertices joining the ends of the sides. An angle is described at each of the vertices, which can have any opening smaller than 90 °.

The sum of its interior angles is equal to 180 °, and the sum of its exterior angles is equal to 360 °.

Triangles are classified according to two main criteria: their sides and their angles.

According to their Sides, the Triangles are going to be Equilateral, Isosceles, Scalenes.

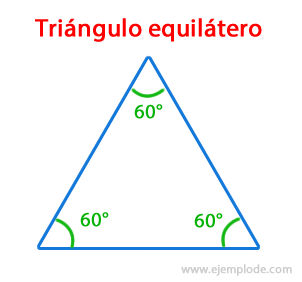
The Equilateral Triangles They have 3 sides of the same measure, which means that their three internal angles are 60 ° each, exactly.

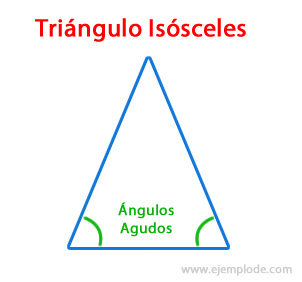
The Isosceles Triangles they have 2 of their equal sides and the other one of different measure. This is why the equal sides will generate 2 equal angles at their ends, already joined by the third side.

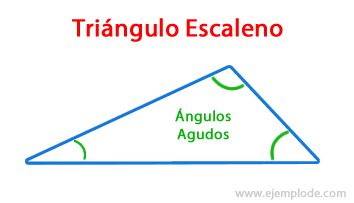
The Scalene Triangles they all have different sides, so all of their internal angles are going to be different.

According to their Angles, the Triangles are going to be Acute Angles, Rectangles and Obtusangles.

The Acute Triangles they have all their acute angles, of course adding 180 °.

The Right Triangles They have a Right angle, that is, 90 °. The others would be the ones who would complete the 180 °. The Right Triangles are the object of analysis of Trigonometry, and are one of the main tools to interpret the reality that surrounds us.

The Obtusangle Triangles they have an obtuse angle, that is, greater than 90 °. The other angles complete the internal 180 °.

Right Triangles

In Right Triangles, each side has a name that is focused on the right angle that characterizes the polygon. The two shorter sides, and that form the Right angle, are called Legs. The longest leg is assigned the letter A, and the shorter leg is called Leg B.

The side facing the Right angle is called Hypotenuse, and unites the two legs.

The sides have quotients to each other, with respect to an angle of the Triangle, generating the so-called Trigonometric Relationships. Among them are:

Breast: Quotient of the Opposite Leg of the Hypotenuse

Cosine: Quotient of the Adjacent Leg to the Hypotenuse

Tangent: Quotient of the Opposite Leg between the Adjacent Leg

Cosecant: Quotient of the Hypotenuse between the Opposite Leg.

Drying: Quotient of the Hypotenuse between the Adjacent Leg.

Cotangent: Quotient between Adjacent Leg and Opposite Leg.

Examples of Characteristics of Triangles

It is a three-sided polygon

The sum of its internal angles is equal to 180 °

The sum of its exterior angles is equal to 360 °

It can be considered as a component of all other polygons

Equilateral Triangles have 3 sides of the same measure

Isosceles Triangles have 2 of their equal sides

The Scalene Triangles have all their different sides

Right Angle Triangles have a Right Angle

Acute Angle Triangles have all their acute angles

Oblong Triangles have an obtuse angle