Linear Function Example

The linear function expresses the relationship between the value of two variables, which is direct and proportional. It is called a linear function since when representing these values ​​in a Cartesian plane the result is a straight line.

A mathematical function is a relationship between two sets of values, which can be represented by equation and graphed on a Cartesian plane The result of the function is represented as f (x), and is read function of x. These relationships can be direct, inverse. Direct relationships are those in which when one quantity increases, the other also increases, and if one quantity decreases, the other also decreases. Inverse relationships are those in which, as one quantity increases, the other decreases, or, conversely, when one decreases the other increases.

One of the most common uses of linear functions is the representation of the relationship between time and the distance that a car travels.

For example, if we know that a car has a speed of 30 km / h, and we want to know the distance it travels in a certain time, we can represent it by means of an equation.

In the equation we will represent the values ​​with letters. In this case, we represent the distance with the letter d; Velocity with the letter v, and time with t. So we will have:

d = v * t

Since we know that the speed is constant, 30 km / h, then our variables will be d and t:

d = 30 * t

To represent this equation as a function, we substitute the letter for the function, since it represents the result of the function, which will depend on the value of t:

f (x) = 30 * t

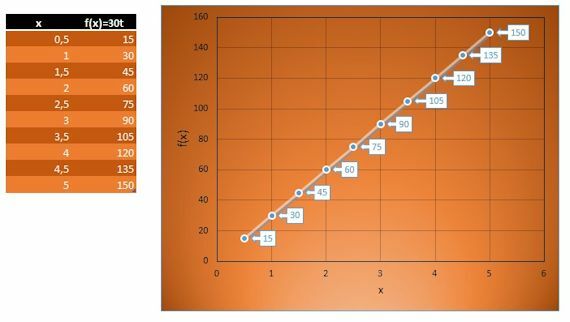
From this we can build a table, where we will put the values ​​that the function f (x) acquires, or that is, the distance traveled, as the value of x varies, which in this case is the time represented by t. In this example, we will measure it in half hours, that is, 0.5 hours.

Once the table of values ​​is obtained, when making a graph in a Cartesian plane, we observe that the graph has the shape of a straight line:

The general formula for linear equations is as follows:

f (x) = ax + b

About the general formula, we can make the following observations:

• Linear equations are always equations of the first degree, that is, they do not have exponents in their members.
• The value of b is constant in the equation. When its value is 0, we only have the value of ax. (as in our example: f (x) = ax + b = 30 * t + 0 = 30 * t)
• The value of a is a constant value. In the example, being a direct variation relation, we can see that a is always the result of dividing f (x) by x (90/3 = 120/4 = 30).

3 examples of linear equation:

Example 1

Now we will take as an example the equation:

y = 5m + 3

By converting it to a function, we get:

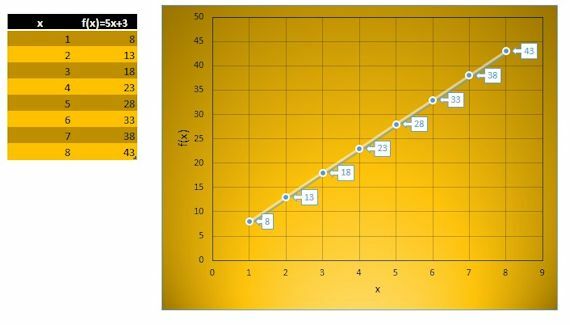
f (x) = 5x + 3

We will assign x values ​​from 1 to 8, and we will make the graph:

Example 2

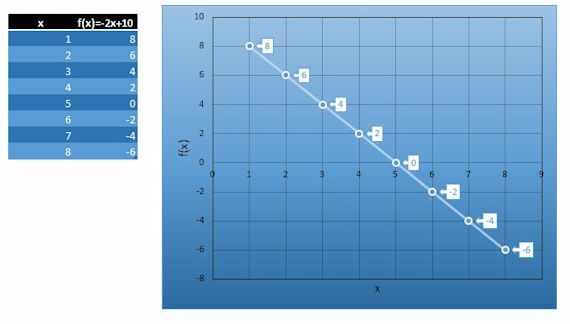
Make the function, table and graph for the equation: y = -2x + 10

f (x) = -2x + 10

We make our table and its graph: