Union Of Sets Example

It's known that a set is a group of elements that have a characteristic in common, by which the difference with other elements and groups becomes clear. Sets have functioned in mathematics as a concept that serves to establish statistics or measures of the common characteristic. For example, to count how many elements are in each set, and compare both sets to see which one is greater.

The Universe is what contains everything; In other words, it is what inhabit all the elements that can be grouped and those that cannot be grouped. Within the Universe there will be all possible sets and loose elements. The Universe will be represented by a rectangle, as a sign that it has a limit, with all the elements inside.

To graphically define a set within the Universe, a circle is drawn inside the rectangle and all the elements that compose it are written inside it. The elements that do not have the common characteristic are left written in the rest of the area of ​​the rectangle, thus indicating that they do not belong to the defined set.

The same will be done if there is a second and a third set, to observe the circles within the Universe, containing their respective elements.

But the time will come when two or three sets have elements that meet two or three characteristics in common, thus giving the partial union of the sets.

Venn Diagram

The Venn Diagram is the tool to represent the union of sets par excellence. The circles of the sets overlap to generate an intermediate area, called Intersection, which is the one that represents the elements that meet the characteristics of both sets at the same weather.

The Venn Diagram, for specific cases, is intended to offer graphical help when estimating the number of elements in one of the sets when not all the data is available.

Examples of Union of Sets

Example of union of two sets

There is a group of 30 people (universe), who are asked if they prefer Classical Music or the Rock genre. 10 respond that they like only Rock, 4 prefer classical music exclusively, and it turns out that the other 16 people have an equal taste for both. The sets and the intersection would be represented as follows:

Example of joining two sets of preferences

To do a survey in movie theaters about the preferred flavors of popcorn, 150 people were taken. The flavors offered were Butter and Caramel. Of those surveyed, 70 in total responded with a liking for those from Butter. If 93 people get together who like both, and there are 20 who only like Caramelo, you can already find out how many have exclusive taste for those of Mantequilla, not counting those of the intersection, and in the end the total number of those who like those of Candy. The diagram looks like this:

For the solution of this diagram, put the data given in the problem. The number 70 of those who have a taste for those of Mantequilla we place it next to the name of the group, to represent its total. The 93 people who like both will go at the intersection. The 20 people who have exclusive taste for Caramel flavor, will go in the circle section that only indicates Caramel.

Adding the Intersection = 93, and the Candy section = 20, we have as a result 113, which are the elements counted so far. We know that the universe U = 150, are the total elements. The difference between the Universe U = 150 and the elements so far counted = 113, we have as a result = 37, which are the remaining elements, belonging to the Butter section.

To know the total elements in the Candy set, we will first know the Butter elements present in the intersection. It is known to be 70 Butter elements. And 37 of them are unique taste. The difference between them is = 33. There are 33 Butter elements present in the Intersection. So we can already know the number of Caramel elements in the Intersection. 93 – 33 = 60. There are 60 Candy elements locked in the Intersection. Added to the 20 of the exclusive Caramelo, it will be known that the Caramelo set has a total of: 60 + 20 = 80 elements.

Example of union of two sets of people

For an addiction research work, a survey was established to find out the number of people who smoked, drank alcoholic beverages, or did both. The group that was handled was 300 people. It was noted that 203 people converged on a double practice of vices; 45 people were exclusively dedicated to Smoking. And in the group of alcoholics there were 112 elements. This is how the current case would be represented:

To solve this case, you can first know the total number of items in the Smoking set. If we know that the Universe consists of 300 people, and there are already 112 in the Alcohol set, by difference we can know that there are 300 - 112 = 188 people in the Smoking set.

To know the number of elements Smoking at the Intersection, we only make the difference of 188 total minus the 45 exclusive ones. 188 – 45 = 143. There are 143 Smoking items at the Intersection.

So, subtracting them from the 203 elements of the Intersection, there are 203 - 143 = 60 elements. There are 60 Alcohol elements in the Intersection. Thanks to this calculation, and subtracting from the 112 totals, it will be possible to know the exclusive elements of Alcohol.

112 – 60 = 52. There are 52 people who only drink alcoholic beverages. Thus, the diagram is already solved.

Example of union of three sets 

On the occasions when there are three working sets, more Intersections will be generated that will relate them to each other. Also, a general intersection of the three sets will result in the center of the diagram.

A reading group is going to be studied to find out the literary preferences of its members, including Novel, Short Story and Short Stories. The group or universe consists of 40 people.

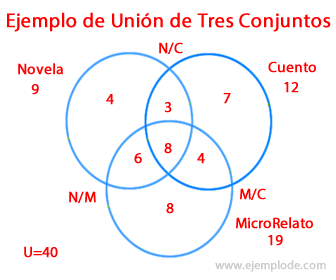
The data collected has been placed in the Venn Diagram, divided into the universe of 40 people. It is known then that 9 people in total have a taste for the Novel, 12 for the Story and 19 for the MicroRelato. Within these three sets, 4 have an exclusive taste for the Novel, 7 have a unique taste for the Story, and 8 only like the MicroRelato.

There are people who have a taste for Novel and Short Story at the same time, which is the Intersection N / C = 3 people. Those who like Story and Micro Story at the same time, the M / C Intersection are 4 people. And those who have a simultaneous taste for Novela and MicroRelato, at the N / M Intersection, are 6 people.

Finally, it was 8 people who had a taste for all three concepts at the same time.

Example of union of three sets of preferences

A buffet restaurant wanted to expand its repertoire and surveyed 250 customers to see what majority preference there was between Japanese food, Mexican food, and Italian food. The Venn diagram was as follows:

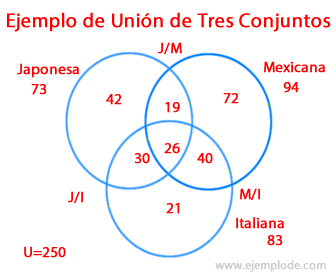
Interpreting the diagram, the result was the following: there are 73 people who have a taste for food Japanese, 94 people with a taste for Mexican food, and 83 people who have a taste for Mexican food Italian.

There are people who have a unique taste for each type of food. There are 42 people who like only Japanese food. There are 72 people who like only Mexican food. And there are 21 people who have a taste for Italian food only.

Within the Japanese, Mexican and Italian ensembles, there are people who have mixed tastes, who combine either two of them or all of them.

There are 19 people who like Japanese and Mexican food. There are 40 people who like Mexican and Italian food. There are 30 people who like Japanese and Italian food. And there are 26 people who like all three foods, Japanese, Mexican and Italian alike.