Compound Rule Of Three Example

A Rule of three It is a mathematical tool that allows knowing a data that is proportional to others offered in the problem. When it comes to a Simple Rule of Three, only two different quantities are covered, with their respective initial and final values, resulting in four data: three for work and one as unknown.

In the case of a Composite Rule of Three, there are more than two magnitudes in the problem, but a single unknown piece of data remains.

The general procedure for its solution consists of the following:

First, you need to sort the data in a table.

Second, you have to define what kind of proportionality connects to the data.

It can be about Direct proportionality, if the increase or decrease of a value corresponds to the same change in the other magnitude. On the other hand, there may be Inverse proportionality, if when one magnitude increases or decreases, the other undergoes an opposite change.

Then, the proportional relationship between all the data is established, to proceed to calculate the missing element.

According to the type of Proportion that the data has, the Composite Rule of Three to be applied will acquire a name: Direct Compound Rule of Three if all magnitudes behave in direct proportion; Inverse Compound Rule of Three if all magnitudes behave with an inverse proportion; and Mixed Compound Rule of Three, when both types of proportionality are present between the magnitudes. Examples of each type of Compound Rule of Three will be cited below.

Direct Compound Rule of Three 

The Direct Proportionality Relationship is written according to the following expression:

Example 1 

8 valves open for 10 hours a day have thrown a quantity of water, with a value of 400 pesos. It is required to know the Discharge Price of 16 valves open 12 hours during the same days.

Setting the reference variable, which is the Price of Discharge, the Proportions of the other magnitudes with respect to it are analyzed:

The Higher the Number of Valves, the Higher the Discharge Price. Direct ratio.

The Higher the Number of Hours per day, the Higher the Discharge Price. Direct ratio.

Then the data will be organized in a table:

8 valves	10 hours a day	400 pesos
16 valves	12 hours a day	X (unknown data)

Knowing that the Proportion is Direct, we proceed to make the mathematical arrangement for the solution, multiplying Directly the known elements, and equating them to the relation of magnitudes in which the unknown:

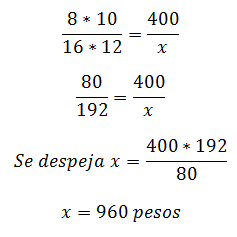
Example 2

Ten vendors have average sales of 400 items, with a final value of 30,000 pesos per week. It is required to estimate the value of the sale for thirty-five sellers with average sales of 1500 items.

The Greater the Number of Sellers, the Greater the Value of the Sale. Direct proportionality.

The Higher the Number of Items Sold, the Higher the Value of the Sale. Direct proportionality.

Then the data will be organized in a table:

10 vendors	400 items	$30,000
35 vendors	1500 items	X (unknown data)

Knowing that the Proportion is Direct, we proceed to make the mathematical arrangement for the solution, multiplying Directly the known elements, and equating them to the relation of magnitudes in which the unknown:

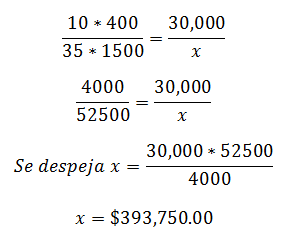
Inverse Compound Rule of Three

The Inverse Proportionality Relationship is written according to the following expression:

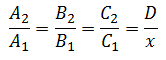
Example

4 Workers work 5 hours a day constructing a building in 2 days. You need to know how long it will take 3 workers working 6 hours a day to build an identical building.

Setting the variable of Days of Tardiness as a reference, the type of proportionality between the data is discovered.

The fewer workers there are, the more days there are late. Inverse proportionality.

The More Daily Hours of work there are, the fewer days late. Inverse proportionality.

Then the data will be organized in a table:

4 Workers	5 hours a day	2 days late
3 Workers	6 hours a day	X (unknown data)

And knowing that the Proportion is Indirect in all cases, we proceed to make the mathematical arrangement to solve the unknown.

Mixed Compound Rule of Three

The Mixed Proportionality Relationship can be written according to the following expression:

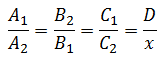
Example 

If 8 workers build a 30-meter wall in 9 days, working at a rate of 6 hours per day, how many days they will need 10 workers working 8 hours a day to build another 50 meters of wall that missing?

Setting the reference variable in Days of Tardiness, we proceed to analyze the proportionality:

The more workers, the fewer days of delay. Inverse proportionality.

The more hours, the less days late. Inverse proportionality.

The more meters of construction, the more days of delay. Direct proportionality.

Then the data will be organized in the table:

8 Workers	9 days late	6 hours	30 meters
10 Workers	X (unknown data)	8 hours	50 meters

We proceed to make the mathematical arrangement to solve the unknown, taking into account the proportionality in each case. If Proportionality is Direct, the position of the number in the table is respected to place it in the numerator or denominator. And when the Proportionality is Inverse, its position is changed when multiplying, to the denominator or numerator, as the case may be.