Example of Rotational And Translational Equilibrium

Equilibrium conditions: For a body to be in equilibrium, it is required that the sum of all the forces or torques acting on it is equal to zero. It is said that every body has two types of balance, that of translation and that of rotation.

Translation: It is the one that arises at the moment when all the forces that act on the body are nullified, that is, the sum of them is equal to zero.
ANDFx = 0
ANDFy = 0

Rotation: It is the one that arises at the moment when all the torques that act on the body are null, that is, the sum of them is equal to zero.
ANDMx = 0
ANDMy = 0

Applications: It is used in all types of instruments in which it is required to apply one or more forces or torques to carry out the balance of a body. Among the most common instruments are the lever, the Roman balance, the pulley, the gear, etc.

EXAMPLE OF APPLICATION PROBLEM:

An 8 N box is suspended by a 2 m wire that makes a 45 ° angle with the vertical. What is the value of the horizontal forces and in the wire so that the body remains static?
The problem is first visualized as follows:

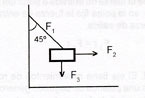
Your free-body diagram is drawn below.

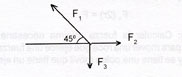
Now by decomposing the vectors, we calculate the force of each of them.

F_1x = - F₁ cos 45 ° *
F_1y = F₁ sin 45 °
F_2x = F₂ cos 0 ° = F2
F_{2 and} = F₂sin0 ° = 0
F_3x = F₃cos90 ° = 0
F_3y = - F₃ sin 90 ° = - 8 N *

Because the quadrants in which they are located are negative.
Since we only know the values ​​of F₃, F₂ and the sum must be equal to zero in x and y, we have the following:

ANDF_x= F_1x+ F_2x+ F_3x=0

ANDF_Y= F_1y+ F_{2 and}+ F_3y=0

Therefore we have the following:

ANDF_x= -F₁ cos 45 + F₂=0
F₂= F₁(0.7071)
ANDF_Y= -F₁sin45-8N = 0
8N = F₁(0.7071)
F₁= 8N / 0.7071 = 11.31 N

To calculate F₂, F is replaced₁ from the following equation:

F₂= F₁(0.7071)
F₂= 11.31 (0.7071) = 8N