Heat Conduction Example

Driving is together with convection and the radiation, one of the three heat transfer mechanisms. It is the transfer of energy from the more energetic particles of a substance to the adjacent less energetic ones, as a result of interactions between these particles. Conduction can take place in any physical state, be it solid, liquid or gas. In gases and liquids, conduction is due to collisions and diffusion of molecules during their random motion. In solids it is due to the combination of the vibrations of the molecules in a lattice and the transport of energy by free electrons. For example, there will come a time when a cold canned drink in a warm room warms up to room temperature. as a result of heat transfer by conduction, from the room to the beverage, through the aluminum that makes up the can.

The speed of heat conduction through a medium depends on the geometric configuration of this, its thickness and the material of which it is made, as well as the temperature difference across he. It is known that wrapping a hot water tank with fiberglass, which is an insulating material, reduces the rate of heat loss from that tank. The thicker the insulation, the lower the heat loss. It is also known that a hot water tank will lose heat at a higher rate when the temperature of the room where it is housed is lowered. Also, the larger the tank, the greater the surface area and consequently the rate of heat loss.

A steady state conduction (which remains constant and without apparent fluctuations) of heat can be considered through a large flat wall of thickness Δx = L and area A. The difference in temperature from one side of the wall to the other is ΔT = T₂-T₁. Experiments have shown that the rate of heat transfer Q through the wall doubles when the difference in Temperature ΔT is doubled from one to another side of it, or, the area A perpendicular to the direction of heat transfer is doubled, but it is halved when the thickness L of the Wall. Therefore, it is concluded that the Speed ​​of Heat Conduction through a flat layer is proportional to the difference of temperature through it and to the area of ​​heat transfer, but it is inversely proportional to the thickness of that layer; is represented by the following equation:

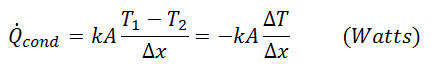
Where the constant of proportionality k is the Thermal conductivity of the material, which is a measure of a material's ability to conduct Heat. In the limiting case of Δxà0, the previous equation reduces to its differential form:

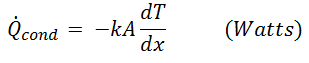
The differential manifestation is called Fourier's Law of Heat Conduction, in honor of J. Fourier, who first expressed it in his text on heat transfer in 1822. The dT / dx part is called Temperature Gradient, which is the slope of the temperature curve on a T-x diagram, that is, the rate of change of Temperature with respect to x, the thickness of the material, at location x. In conclusion, Fourier's Law of Heat Conduction indicates that the rate of heat conduction in one direction is proportional to the temperature gradient in that direction. Heat is conducted in the direction of decreasing temperature and the temperature gradient becomes negative when the latter decreases with increasing x. The negative sign in the equations guarantees that the heat transfer in the positive x direction is a positive quantity.

The area A of heat transfer is always perpendicular to the direction of that transfer. For example, for heat loss through a wall that is 5 meters long, 3 meters high, and 25 centimeters thick, the heat transfer area is A = 15 square meters. It should be noted that the thickness of the wall does not affect A.

Thermal conductivity

 The great diversity of materials store heat differently and the property of Specific Heat C has been defined._P as a measure of a material's ability to store thermal energy. For example, C_P= 4.18 kJ / Kg * ° C for water, and 0.45 kJ / Kg * ° C for iron, at room temperature, indicates that water can store almost 10 times more energy than iron per unit mass. Similarly, thermal conductivity k is a measure of a material's ability to conduct heat. For example, k = 0.608 W / m * ° C for water, and 80.2 W / m * ° C for iron, at room temperature, indicates that iron conducts heat more than 100 times faster than water. Therefore, water is said to be a poor conductor of heat relative to iron, even though water is an excellent medium for storing thermal energy.

It is also possible to use Fourier's Law of Heat Conduction to define thermal conductivity as velocity heat transfer through a unit thickness of the material per unit area per unit temperature difference. The thermal conductivity of a material is a measure of the material's ability to conduct heat. A high value for thermal conductivity indicates that the material is a good conductor of heat, and a low value indicates that it is a poor conductor or that it is a Insulating thermal.

Thermal diffusivity

 Another property of materials that participates in the analysis of heat conduction in a transitory regime (or changing) is thermal diffusivity, which represents how fast heat diffuses through a material and is defined as go on:

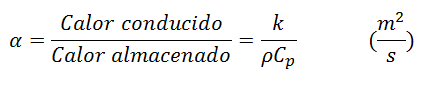
Being the k of the numerator the thermal conductivity, and the product of the denominator of the density of the substance by the specific heat represents the heat capacity. Thermal conductivity shows how well a material conducts heat, and Heat Capacity represents how much energy a material stores per unit volume. Therefore, the thermal diffusivity of a material can be conceived as the ratio between the heat conducted through the material and the heat stored per unit volume.

A material that has a high thermal conductivity or a low heat capacity ultimately has a high thermal diffusivity. The higher the thermal diffusivity, the faster the heat propagation to the medium. On the other hand, a small value of thermal diffusivity means that, for the most part, the heat is absorbed by the material and a small amount of that heat will be conducted further.

For example, the thermal diffusivities of beef and water are identical. The logic lies in the fact that meat, as well as fresh vegetables and fruits, are made up for the most part of water, and consequently have its thermal properties.