Example of Pascal's Principle

When the French scientist and philosopher Blaise Pascal studied fluids, both at rest and in motion, one of his most interesting observations and that has become one of the basic principles of the study of physics, is the called "Pascal's Principle", Which says that:

"The pressure exerted on a point in an incompressible liquid that is in a closed system, is transmitted in all directions of the fluid constantly."

To clarify this principle, we must understand some concepts:

System closed

It is when the liquid is in a container, container or pipe, which prevents the liquid from escaping through a place other than the spaces provided for the exit of the liquid. However, it must be borne in mind that when there is excessive pressure, the resistance offered by the container can be exceeded and break it.

Pressure

It is a force exerted on a surface of the liquid that we are considering.

Incompressible liquid

A liquid is said to be incompressible when it cannot be compressed, that is, when applying pressure to it in a closed system, we cannot reduce its volume. To understand this concept, we can exemplify it with a syringe. If we take a syringe and remove the needle, then fill it with air, cover the outlet hole and push the plunger, we can realize that the air is compressed to a critical point where we can no longer push the plunger and we have not reached the end of its travel either, because the air has been compressed to a point that can no longer be compressed more. Air is a compressible fluid. On the other hand, if we repeat this experience, but filling the syringe with water, we will realize that once we fill the syringe, we can no longer push the plunger.

Water is an incompressible fluid.

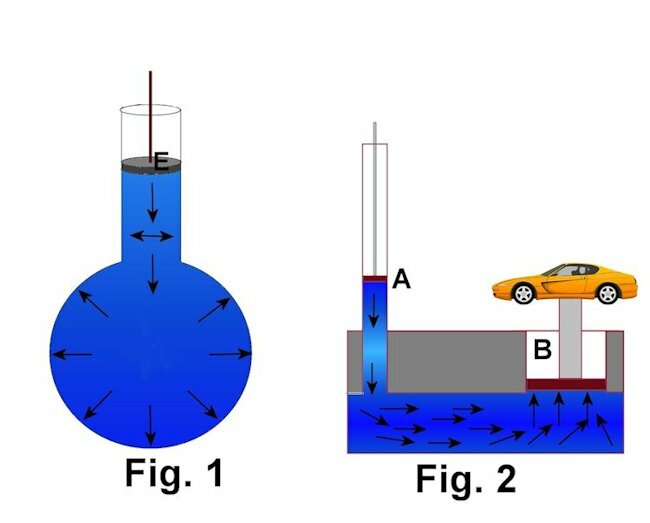
If we have a container like the one in figure 1, and we apply a force on the piston E, the pressure will be evenly distributed throughout the liquid, and at any point in the container will have the same Pressure.

Formulas and Units of Measure

The pressure applied through a plunger can be measured in various ways. One of the most common is by grams per square centimeter in the metric system (g / cm²), or pounds per square inch in the English system (psi).

In the international system of weights and measures, fluid pressure is measured in a unit called Pascal, which is the measurement resulting from applying a force of one Newton applied to a surface of one meter square:

1Pa = 1N / m²

And one Newton is equal to the force necessary to move a 1kg mass giving it an acceleration of 1 meter per second:

1Pa = 1N / m² = 1 kg / m * s²

Pascal's principle has its practical application in the transmission of a force through a liquid by means of pressure applied to a piston, which is transmitted to another piston. To apply it, we begin by understanding that the pressure applied to the surface of plunger 1 is the same pressure that is transmitted to the surface of plunger 2:

p₁= p₂

The forces are calculated from the multiplication of the pressure applied by the surface on which it acts. Since one of the pistons is smaller, the force on that piston will be less than the force on the larger piston:

F₁= p₁S₁ 

1S₂ = p₂S₂ = F₂

Explaining this formula, we have that Force 1 (F₁), is equal to the product of pressure 1 by the surface of piston 1 (p₁S₁). Since this is the smallest piston, the value of force 1 is less (1S₂), and since pressure 2 is equal to pressure 1, then pressure 2 multiplied by surface 2 (p₂S₂) is equal to Force 2 (F₂).

From this general formula, we can calculate any of the values, knowing some of the others:

F₁= p₁S₁
p₁= F₁/ S₁
S₁= F₁/ p₁
F₂= p₂S₂
p₂= F₂/ S₂
S₂= F₂/ p₂

We will use figure 2 as an example.

Piston A is a 20 cm diameter circle, and piston B is a 40 cm diameter circle. If we apply a force of 5 Newtons on the piston, let's calculate what pressure is produced and what is the resultant force on piston 2.

We begin by calculating the area of ​​the emboli.

Plunger A:
 20 cm in diameter, which is equal to 0.2 meters. As the area of ​​the circle:

1. A = pr²

Then:

A = (3.14) (.1²) = (3.14) (0.01) = 0.0314 m²

We calculate the large plunger:

A = (3.14) (.2²) = (3.14) (0.04) = 0.1256 m²

Now we calculate the pressure produced, dividing the Force of the plunger A by its surface:

p₁= 5 / .0314 = 159.235 Pa (Pascals)

As p₁= p₂, we multiply it by Surface 2:

F₂= p₂S₂
F₂= (159.235) (0.1256) = 20 Newtons

Applied example of Pascal's principle:

Calculate the force and pressure exerted on a piston, if we know that the resultant force is 42N, the larger piston has a radius of 55 centimeters and the smaller piston has a radius of 22 centimeters.

We calculate the surfaces:

Major plunger:

(3.14) (.55²) = (3.14) (0.3025) = 0.950 m²

Minor piston:

(3.14) (.22²) = (3.14) (0.0484) = 0.152 m²

We calculate the pressure:

F₂= p₂S₂,
So that:
p₂= F₂/ S₂
p₂= 42 / .950 = 44.21 Pa

We calculate the applied force:

F₁= p₁S₁
F₁= (44.21) (0.152) = 6.72 N