Example of Addition and Subtraction of Forces

In the addition and / or subtraction of vector forces, the vector that is obtained is called the resultant vector, to calculate it the following graphical or analytical methods can be used:
Graphic methods: In graphical methods it is of utmost importance to determine a standard measure for the magnitude of the vector and preferably use graph paper or graph paper for a better vector calculation resulting.
Triangle method: The first vector V is placed₁ with their respective measurements, once graphed, the second vector V is placed₂ with their respective measurements, placing the starting point of the vector at the tip of the first arrow. Finally, a vector V is drawn_r from the starting point of the first to the point of the arrow of the second. The resulting vector will be equal to the sum of the two vectors, the direction angle is taken with a protractor and the direction is observed with the arrowhead.

EXAMPLE OF APPLICATION PROBLEM:

Join forces ^→F₁ = 16 m / s, 45 ° east direction upwards, with vector ^→F₂= 8m / s, 90 ° eastbound clockwise.

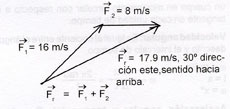
Analytical method: It is based on the decomposition of force into its components on both the X and Y axes. To calculate the value of the force in its axes we take as a basis the following formulas:
^→F_X=^→Fcost ^→F_Y=^→Fsent
EXAMPLE OF APPLICATION PROBLEM:

The force of a car was 20 N, with an angle of 60 ° with an east-west direction and upwards. Calculate the resultant force.
For the force at X, the cosine of 60 ° is equal to: 0.5.
^→F_x = ^→F cos to = 20 km x 0.5 = 10 km
For the force at Y, the sine is equal to: 0.866
^→F_Y= ^→Fsen to = 20 km x 0.866 = 17.32 km
Once the following is done, the calculation of the resulting vector is carried out by means of the Pythagorean theorem.

Finally, the angle is determined by means of the following formula:

to= tg^-1→F_Y / ^→F_x= 17.32 / 10=60°