Free Fall Example

The freefall It exists when a body is released from a height X, with an initial velocity of zero and during the fall it acquires acceleration due to the force of gravity.

The freefall of bodies is a physical magnitude that refers to a movement with a vertical direction downwards, starting from rest (initial speed = 0), and ideally without any obstacle or circumstance that slows the movement. All bodies fall with the same speed in a vacuum. In air, this property is noticeable for heavy bodies, but not for light bodies, such as a tree leaf or a paper, because the air produces friction, offering a resistance that slows the acceleration movement of the fall free.

Free Fall is a uniformly accelerated motion. For practical purposes, we do not take into account the effect of air friction. To do the free fall calculations, we use a constant and three variables. The constant is the acceleration value of gravity (g) which is g = 981cm / s² or g = 9.81m / s². This means that a body will accelerate 9.81 meters every second. The first variable is the final speed (v

_or or v_F), which is the speed that the object reaches at the end of the journey. Another variable is time (t), which is how long it takes to travel from the starting point to the end of the journey. The third variable is the height (h), which is the distance from the starting point to the end of the route.

As we can see, free fall has the same components as Uniformly Accelerated Motion (MUA), and the formulas are equivalent:

MUA <> FREE FALL
Acceleration (a) <> gravity (g)
Initial velocity (v_or) <> Initial velocity (v_or)
Fine speed (v_F) <> final velocity (v_F)
Distance (d) <> height (a, h)
Time (t) <> time (t)

Likewise, the formulas for solving the variables for free fall correspond to those for uniformly accelerated motion.

MUA <> FREE FALL
Final speed (for an initial speed of 0):
V_F= a * t <> v_F= g * t
Time (for a starting speed of 0):
t = v_F / a <> t = v_F/ g
Height (for an initial velocity of 0):
d = ½ at² <> h = ½ gt²

Free fall can be combined with an initial push. In this case both movements are added, following the formulas of the uniformly accelerated movement:

MUA <> FREE FALL
Final speed:
V_F= v_or + (a * t) <> v_F= v_or + (g * t)
Weather:
t = (v_F - v_or) / a <> t = (v_F- v_or) / g
Alters:
d = v_ort + (½ at²) <> h = v_ort + (½ gt²)

The conventional units for each element are:

g = m / s²
v_or = m / s
v_F = m / s
h = m
t = s

In addition, graphs can be constructed from each of the variables. The time and acceleration graphs will be progressive straight lines in the Cartesian plane, while the distance graphs will be curved.

Examples of free fall problems:

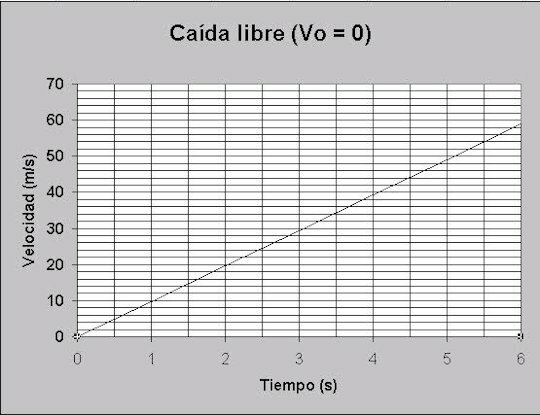
Problem 1: Calculate the final speed of an object in free fall, which starts from rest and falls for 5.5 seconds. Build graph.

V_or = 0

g = 9.81 m / s2

t = 5.5 s

Formula v_F= g * t = 9.81 * 5.5 = 53.955 m / s

Problem 2: Calculate the final velocity of an object in free fall, with an initial impulse of 11 m / s and falls for 7.3 seconds. Build graph.

V_or = 11

g = 9.81 m / s2

t = 7.3 s

Formula = v_or + (g * t) = 11 + (9.81 * 7.3) = 82.54 m / s

Problem 3: Calculate the height from which a free-falling object was thrown, which took 6.5 seconds to hit the ground. Build graph.

V_or = 0

g = 9.81 m / s2

t = 6.5 s

formula = h = ½ gt² = .5* (9.81*6.5²) = .5 * 414.05 = 207.025 m

Problem 4: Calculate the height from which an object in free fall was thrown, with an initial velocity of 10 m / s, which took 4.5 seconds to hit the ground. Build graph.

V_or = 10

g = 9.81 m / s2

t = 4.5 s

Formula = h = v_ort + (½ gt²) = (10*4.5) + (.5*[9.8*4.5²]) = 45 + .5* (9.81*6.5²) = 45 + (.5 * 198.45) = 45 + 99.225 = 144.225 m