Example of Ideal and Real Gases

A Ideal gas is the one whose properties like Pressure, Temperature and Volume covered, they keep always a proportion or constant relationship between them. In other words, its behavior follows the Ideal Gas Law, which is represented as follows:

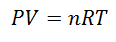
To arrive at this formula, we start from La General Law of the Gaseous State, which describes that there is a constant relationship between the properties of the gas at all times in a process. The properties that are talked about are the Pressure in the system where the gas is, the Volume that occupies the gas, and the Temperature of gas.

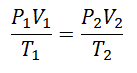
It was decided sooner or later to form a simpler expression, giving the constancy a letter to accompany the expression:

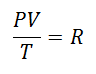
It was called Universal Gas Constant at factor R, and its value is the following:

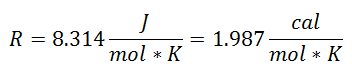
And since the Universal Gas Constant applies for each mole of the gas, the Number of Moles of Gas as one more factor, to cover all the substance present in the system during the process. We will already have the final equation in this form:

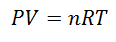
The above equation is Ideal Gas Law, and applies to gases that are at a temperature between moderate and high. Thus, any of the variables can be calculated, having the others determined.

Difference between Ideal Gases and Real Gases

This Ideal Gas Law does not apply for gases that are at low temperatures or close to the point where they become liquid.

Low temperatures result in a less particle movement gas, and these will settle more, occupying a different volume than when they were completely dispersed.

In addition, for the same reason, they would be exercising a Uneven pressure throughout the system. Proportionality will start to fail and the formula will not have the same validity for calculations.

In that case, equations for Real gases should be used.

A Real Gas is the one whose properties they do not comply in relating exactly as in the Ideal Gas Law, so the way of calculating these properties is modified.

Equations of State for Real Gases

1.- Virial Equation:

For a gas that stays at Constant Temperature, the relationship between Pressure and Volume or Pressure and specific volume (volume occupied by each unit of mass of the gas).

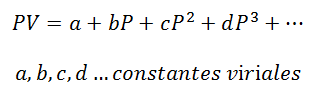
Virial constants are characteristics of each gas, with specific values ​​that depend on Temperature.

Only pressure and volume calculations can be made; Temperature is previously determined by observing the process. For these calculations the variables of the virial equation are cleared:

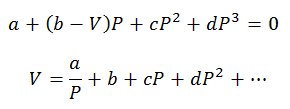
The virial constants to solve the equations are obtained from specialized tables.

2.- EquationVan der Waals on:

The Van der Waals Equation is another expression used to calculate the properties of a Real Gas, and like the Virial Equation, it also requires its constants:

Constants are also queried in tables.

3.- EquationRedli onch-Kwong:

This equation works very well to make calculations with gases at almost any temperature, and average pressures, but without being too high, such as hundreds of atmospheres.

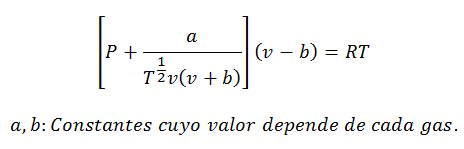
Constants are also queried in tables.

You can clear the Pressure, Temperature and Volume, to make your calculations. Clearances remain:

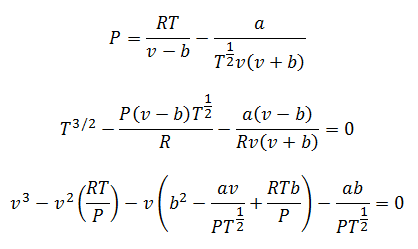
4.-Berthelot equation:

It is possible to calculate any of the variables with this equation. Only it has two different modes: For low pressures and for high pressures.

For low pressures:

For high pressures:

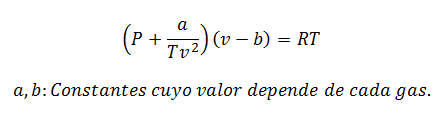
Constants are also queried in tables.

5.-Compressibility Factor Equation

This equation is a simpler variant of the Ideal Gas Law; only the factor "z" is added, called the Compressibility Factor. This factor is obtained from the Generalized Compressibility Factor Graph, depending on either the Temperature, the Pressure or the specific Volume, depending on what is available.

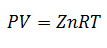
Examples of Ideal and Real Gases

As the ideal or real character It depends on the conditions of Pressure, Temperature in which the Gas is, It is not possible to establish a limited list, so a list of gases is presented, which of course can be found in ideality and reality.

1. Ammonia
2. Refrigerant R134 (DiFluoroDiCloro Ethane)
3. Carbon dioxide
4. Carbon monoxide
5. Oxygen
6. Nitrogen
7. Hydrogen
8. Nitrogen dioxide
9. Dinitrogen Trioxide
10. Dinitrogen pentoxide
11. Dinitrogen Heptoxide
12. Sulfur dioxide
13. Sulfur trioxide
14. Chlorine
15. Helium
16. Neon
17. Argon
18. Krypton
19. Xenon
20. Methane
21. Ethane
22. Propane
23. Butane