Boyle's Law Example

When studying the properties of gases, Robert Boyle, on the one hand, and Edme mariotteOn the other, without knowing or knowing their experiments, they observed that gases can be compressed, and that their volume varies in proportion to the pressure to which they are subjected.

To understand his research, we have to bear in mind that there are three characteristics to take into consideration in this study of gases: temperature, volume and pressure.

Temperature: It is the temperature at which a gas is found under the conditions of the experiment. It can be expressed in degrees centigrade (° C) or in degrees Kelvin or absolute zero (° K). In the case of Boyle's Law, it is considered that the temperature does not vary, that is, it remains constant.

Volume: It is the space that a gas occupies within a closed container. In first intention, the volume of a gas is the volume of the container. For its representation, it is considered that the container is closed and with a plunger, such as a syringe.

Pressure: It is the pressure that the gas has through the plunger. In a closed container, on which the plunger is placed as a lid, without applying pressure, it is considered to be at atmospheric pressure (1 at).

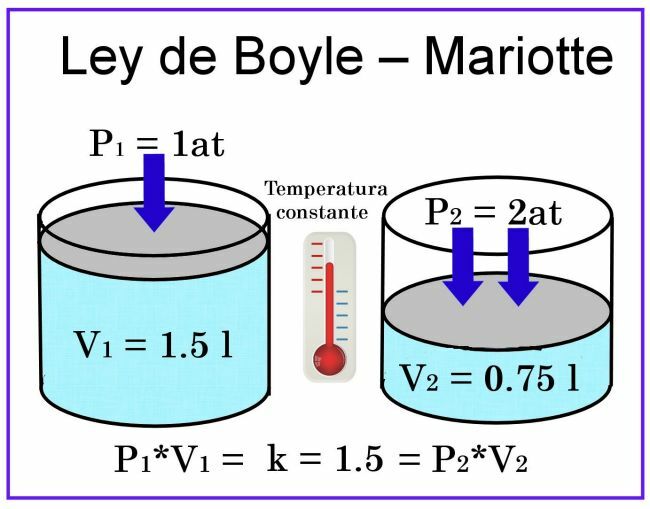
In Boyle and Mariotte's observations, the temperature is considered to be constant, so it will not affect the measurement.

Regarding the volume, if we consider, for example, a cylindrical container of 1 liter capacity, and its lid is a plunger sliding, when placing it covering the container filled with air, the pressure will be 1 at, while the volume will be 1 liter. If a pressure of 2 atmospheres is exerted on the plunger, the volume of the gas will be reduced by half, that is, to 0.5 liters or 500 ml. If the pressure increases to 4 atmospheres, the volume will be reduced to a quarter, that is, to 0.25 liters, or 250 ml.

Based on these observations, the call was enunciated Boyle's Law: At constant temperature, the volume of a gas is inversely proportional to the pressure exerted on it.

This means that when pressure increases, volume decreases, and when pressure decreases, volume increases.

This leads to establish that there is a relationship between the pressure of a gas and its volume, which by varying one of the components, the other varies in the same proportion, the relationship remaining constant, that is say:

P * V = k
P = Pressure
V = Volume
k = constant of the pressure-volume relationship

To understand this, suppose we have a 2.5-liter container, which is filled with air and the pressure on the plunger-cap is 1.5 at. So the constant of your relationship is:

P * V = k = (2.5) (1.5) = 3.75

If we now increase the pressure to 3 atmospheres, we divide k by the pressure P, and we will have:

k / P = V
3.75 / 3 = 1.25 liters

As we see, when applying double the pressure, the volume is half the original, and the constant of the pressure-volume relationship is maintained. This is expressed as follows:

V₁P₁ = V₂P₂ = k

That is, the product of volume 1 times pressure 1 is equal to the product of volume 2 times pressure 2, and this relationship remains constant.

Examples of the Boyle-Mariotte Law

Example 1. Calculate the volume that a gas will occupy, which is occupying a volume of 3.75 liters, at a pressure of 2 at if a pressure of 3.5 at is applied to it.

V₁ = 3.75 l
P₁ = 2 at
V₂ = ?
P₂ = 3.5 at
As V₁P₁ = V₂P₂ = k

We calculate the constant of the system:

V₁P₁= k = (3.75) (2) = 7.5

We solve for V₂:

V₂ = k / P₂ = 7.5 / 3.5 = 2,143 liters

Example 2. Calculate the pressure applied to a gas, if it is occupying a volume of 2.25 liters, if at a pressure of 1.75 at it has a volume of 3.25 liters.

V₁ = 3.25 l
P₁ = 1.75 at
V₂ = 2.25 l
P₂ = ?

We calculate the constant of the system:

V₁P₁= k = (3.25) (1.75) = 5.6875

We solve for P₂:

P₂ = k / V₂ = 5.6875 / 2.25 = 2.53 at

Example 3. Calculate the original pressure of a gas, if when applying a pressure of 4.5 at, it occupies a volume of 1.4 liters, and its original volume was 2.2 liters.

V₁ = 2.2 l
P₁ = ?
V₂ = 1.4 l
P₂ = 4.5 at

We calculate the constant of the system:

V₂P₂= k = (1.4) (4.5) = 6.3

We solve for P₂:

P₁ = k / V₁ = 6.3 / 2.2 = 2.863 at