Concept in Definition ABC

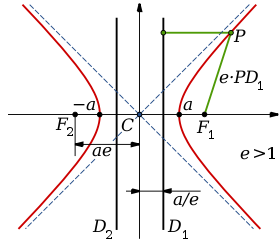At the behest of the Geometry, the hyperbola is that flat symmetric curve with respect to two blueprints perpendicular to each other, while the distance in relation to two points or foci it is constant.

In other words, the hyperbola is a conical section, an open curve with two branches that can be obtained by cutting a right cone through an oblique plane to the axis that imposes symmetry; and with an angle smaller than that of the generatrix with respect to the axis of revolution.

It should be noted that it is the geometric place of the points of a plane, being the absolute value of their distances to two fixed points, the foci, equal to the distance between the vertices, which turns out to be a constant positive.

Meanwhile, the word hyperbola has its origin in the Greek term hyperbole, that literary figure that implies exaggeration as for what was spoken or commented.

As a consequence of the inclination of the cut, the plane of the hyperbola will intersect both branches of the cone.

According to the tradition the discovery of the conic sections are due to the mathematician of Greek origin Menechmus, more precisely in the study that he carried out of the problem of the duplication of the cube he demonstrated the existence of a solution by cutting a parable with a hyperbola, a fact that later would also be demonstrated by Eratosthenes and by Proclus.

In any case, it would be after the above that the term hyperbola as such would be used; Apollonius of Perge in his treatise Conicals was the first to use it. The aforementioned work is considered a masterpiece in the area of math ancient greeks.