Exponenciális függvény definíció

Az exponenciális függvény különféle természeti jelenségeket, társadalmi és gazdasági helyzeteket modellez, ezért is fontos az exponenciális függvények azonosítása különféle összefüggésekben.

Emlékezzünk arra, hogy egy számra \({a^1} = a,{a^2} = aa,\;{a^3} = aaa\) definiálva van, általában minden \(n\) ) természetes szám:

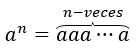
\(a \ne 0\) esetén a következőt kapjuk: \({a^0} = 1,\;\) valójában amikor \(a \ne 0,\) akkor van értelme a \ műveletet végrehajtani (\frac{a}{a} = 1;\) a kitevők törvényének alkalmazásakor a következőket kapjuk:

\(\frac{a}{a} = 1\)

\({a^{1 – 1}} = 1\)

\({a^0} = 1.\)

Amikor \(a = 0\), az előző érvelésnek nincs értelme, ezért a \({0^0},\) kifejezésnek hiányzik a matematikai értelmezése.

Abban az esetben, ha \(b > 0\) és igaz, hogy \({b^n} = a,\), azt mondjuk, hogy \(b\) a \(a\) n-edik gyöke, és általában jelölése \ (b = {a^{\frac{1}{n}}},\;\) vagy \(b = \sqrt[n]{a}\).

Amikor \(a < 0\), akkor nincs \(b\) valós szám, amelyre \({b^2} = a;\), mert \({b^2} \ge 0;\;\ ) így a forma kifejezései \({a^{\frac{m}{n}}}\), nem lesz figyelembe véve \(a < 0.\) A következő algebrai kifejezésben: \({a^n}\) \(a \ ) bázisnak nevezzük, \(n\) pedig az kitevőnek nevezzük, a \({a^n}\) az \(a\) hatványának\(\;n\) vagy \(a\)-nak is nevezik a \(n,\;\)se hatványhoz tartsa be az alábbi törvényeket a kitevők közül:

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\)	\({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\left( {ab} \right)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) minden \(a \ne 0\)

Az exponenciális függvény a következő alakú:

\(f\left( x \right) = {a^x}\)

ahol \(a > 0\) egy állandó, a független változó pedig a \(x\) kitevő.

Az exponenciális függvény elemzéséhez három esetet veszünk figyelembe

1. eset Amikor az alap \(a = 1.\)

Ebben az esetben \(a = 1,\) a \(f\left( x \right) = {a^x}\) függvény egy állandó függvény.

2. eset Amikor az alap \(a > 1\)

Ebben az esetben a következők állnak rendelkezésünkre:

\(x\) értéke
\(x < 0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x} < a\)
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(a < {a^x}\)

A \(f\left( x \right) = {a^x}\) függvény szigorúan növekvő függvény, vagyis ha \({x_2} > {x_1}\), akkor:

\({a^{{x_2}}} > a_{}^{{x_2}}\)

\(f\left( {{x_2}} \right) > f\left( {{x_1}} \right)\)

Ha egy jelenséget exponenciális függvénnyel modelleznek, \(a > 1\), akkor azt mondjuk, hogy exponenciális növekedést mutat.

2. eset Amikor az alap \(a < 1\).

\(x\) értéke
\(x < 0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x} < a < 1\)

Amikor \(a < 1\), a \(f\left( x \right) = {a^x}\) függvény szigorúan csökkenő függvény, vagyis ha \({x_2} > {x_1}\ ), így:

\({a^{{x_2}}} < a_{}^{{x_1}}\) \(f\left( {{x_2}} \right) < f\left( {{x_1}} \right) \) Amikor egy jelenség az Az exponenciális függvényt tartalmazó modellek \(a < 1\) esetén azt mondjuk, hogy ez csökkenést vagy csökkenést mutat exponenciális. A következő grafikon a \({a^x}\) viselkedését szemlélteti három különböző esetben.

Az exponenciális függvény alkalmazásai

1. példa Népességnövekedés

Jelöljük \({P_0}\) a kezdeti populációt és \(r \ge 0\) a népességnövekedési rátát, ha a népesség aránya időben állandó marad; a funkció

\(P\left(t \right) = {P_0}{\left({1 + r} \right)^t};\)

Keresse meg a populációt a t időpontban.

Gyakorlati példa 1

Mexikó lakossága 2021-ben 126 millió volt, és éves szinten 1,1%-os növekedést mutatott. Ha ez a növekedés fennmarad, mekkora lesz a népesség Mexikóban 2031-ben, ebben az évben 2021?

Megoldás

Ebben az esetben \({P_o} = 126\) és \(r = \frac{{1.1}}{{100}} = 0,011\), ezért a következőket kell használnia:

\(P\left(t \jobbra) = {P_0}{\left({1 + .0011} \jobbra)^t}\)

Az alábbi táblázat mutatja az eredményeket

Év	eltelt idő (\(t\))	Számítás	Népesség (millió)
2021	0	\(P\left(t \jobbra) = 126{\left( {1,0011} \jobbra)^0}\)	126
2031	10	\(P\left(t \jobbra) = 126{\bal({1,0011} \jobbra)^{10}}\)	140.57
2051	30	\(P\left(t \jobbra) = 126{\bal({1,0011} \jobbra)^{30}}\)	174.95

2. példa A kamatos kamat kiszámítása

A bankok éves kamatot kínálnak, de a reálkamat attól függ, hogy hány hónapig fekteti be; Ha például r%-os éves kamatlábat kínálnak Önnek, a valós havi kamatláb \(\frac{r}{{12}}\)%, a kéthavi kamat \(\frac{r}{6}\)%, negyedéves \(\frac{r}{4}\)%, negyedéves \(\frac{r}{3}\)%, a félév pedig \(\frac{r}{2}\)%.

Gyakorlati példa 2

Tegyük fel, hogy 10 000-et fektet be egy bankba, és a következő éves kamatokat kínálják:

Lekötött betétek	Éves árfolyam	időszakok egy évben	tényleges árfolyam	\(k\) hónap alatt felhalmozott pénz
Két hónap	0.55%	6	\(\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}\)	\(10000{\left( {1 + 0,00091667} \right)^{\frac{k}{2}}}\)
három hónap	1.87%	4	\(\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}\)	\(10000{\left( {1 + 0,00461667} \right)^{\frac{k}{3}}}\)
hat hónap	1.56%	2	\(\frac{{1,56\% }}{4} = 0,78{\rm{\% }}\)	\(10000{\left( {1 + 0,0078} \right)^{\frac{k}{6}}}\)

A \(e\) szám, Euler állandó és folyamatos kamata.

Most tegyük fel, hogy van induló tőkénk \(C\), és fix kamatláb mellett fektetjük be \(r > 0\), és az évet \(n\) periódusokra osztjuk; az egy évben felhalmozott tőke egyenlő:

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)

Annak elemzésére, hogy a felhalmozott tőke hogyan viselkedik, amikor \(n\), nő, átírjuk a felhalmozott tőkét, egy év alatt:

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)\(A = \;C{\left( {1 + \frac{1} {{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right) r}},\)

a \(m = \frac{n}{r}\) művelettel a következőket kapjuk:

\(A = C{\left( {1 + \frac{1}{m}} \right)^{mr}}\)\(A = C{\left( {{{\left( {1 + \ frac{1}{m}} \right)}^m}} \right)^r}.\)

Ahogy a \(n\) növekszik, úgy nő a \(m = \frac{n}{r}.\)

Ahogy \(m = \frac{n}{r},\) növekszik, a \({\left( {1 + \frac{1}{m}} \right)^m}\) kifejezés megközelíti az ún. Euler-állandó vagy szám:

\(e \kb. 2,718281828 \lpont .\)

Az Euler-állandónak nincs véges vagy periodikus decimális kifejezése.

A következő közelítéseink vannak

\(C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \approx C{e^r},\) \(C{\left( {1 + \frac{r}{n}} \right)^{ns}} \approx C{e^{rs}}.\)

A kifejezéshez:

\(A = \;C{e^r},\)

Kétféleképpen értelmezhetjük:

1.- Egy évben felhalmozható maximális összegként \(C,\;\) éves kamattal tőkét \(r.\)

2.- Az az összeg, amit egy év alatt felhalmoznánk, ha tőkénket folyamatosan, éves ütemben újra befektetnénk \(r.\)

\(T\left(s \right) = \;C{e^{rs}},\)

a felhalmozott összeg, ha \(s\) év folyamatos kamattal történik.

Konkrét példa 3

Most visszatérünk a 2. konkrét példa egy részére, ahol az éves ráta 0,55% kéthavi részletekben. Számítsd ki azt a tőkét, amely felhalmozódik, ha az induló tőke 10 000, és fél év, két év, 28 hónap után újra befektet!

\(10{\left( {1,00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525\)

ahogy az alábbi táblázat is mutatja, a \(m = \frac{n}{r},\) értéke nem „kicsi”, és a fenti táblázat azt jelzi, hogy \({\left( {1 + \frac{1}{ m}} \right)^m}\) közel van az Euler-állandóhoz.

Idő	Időszakok száma (\(k\))	Felhalmozott tőke, ezerben, kéthavonta újra befektetve
Fél év	3	\(10{\left( {1,00091667} \right)^3} = 10.{\rm{\;}}027525\)
Két év	12	\(10{\left( {1,00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 hónap	19	\(10{\left( {1,00091667} \right)^{19}} = 10.\;175612\)

Idő	Az évek ideje (\(s\))	Felhalmozott tőke, ezerben, fektessen be folyamatos kamattal
Fél év	\(s = \frac{1}{2}\)	\(10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\)
Két év	\(s = 2\)	\(10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607\)
38 hónap	\(s = \frac{{19}}{6}\)	\(10{\left( {1,00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

2. példa Értékcsökkenés

Gyakorlati példa 1

Egy számítógép minden évben 30%-ot leértékelődik, ha egy számítógép 20 000 peso dollárba kerül, határozza meg a számítógép árát \(t = 1,12,\;14,\;38\) hónapra.

Ebben az esetben az egyik rendelkezik:

\(P\left(t \jobbra) = 20000{\rm{\;}}{\left( {1 – 0,30} \jobbra)^t}\)

\(t\)-vel években, ha a következő táblázatban \(t\)-t helyettesítjük, az eredményt kap

idő hónapokban	idő években	számításokat	Numerikus érték
1	\(\frac{1}{{12}}\)	\(P\left(t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left(t \jobbra) = 20000{\rm{\;}}{\left( {1 – .30} \jobbra)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left(t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left(t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	6464.0859