Eksponenciālās funkcijas definīcija

Eksponenciālā funkcija modelē dažādas dabas parādības un sociālās un ekonomiskās situācijas, tāpēc ir svarīgi identificēt eksponenciālās funkcijas dažādos kontekstos.

Atcerēsimies, ka skaitlim \({a^1} = a,{a^2} = aa,\;{a^3} = aaa\) ir definēts, parasti tas ir jebkuram \(n\ ) dabiskais skaitlis:

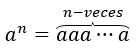
Gadījumā \(a \ne 0\) mums ir šāds: \({a^0} = 1,\;\) patiesībā, kad \(a \ne 0,\) ir jēga veikt darbību \ (\frac{a}{a} = 1;\), piemērojot eksponentu likumu, mums ir:

\(\frac{a}{a} = 1\)

\({a^{1–1}} = 1\)

\({a^0} = 1.\)

Ja \(a = 0\), iepriekšējam pamatojumam nav jēgas, tāpēc izteiksmei \({0^0},\) trūkst matemātiskas interpretācijas.

Gadījumā, ja \(b > 0\) un tā ir taisnība, ka \({b^n} = a,\), tiek teikts, ka \(b\) ir \(a\) n-tā sakne un parasti ir apzīmēts kā \ (b = {a^{\frac{1}{n}}},\;\) vai \(b = \sqrt[n]{a}\).

Ja \(a < 0\), nav tāda reāla skaitļa \(b\), lai \({b^2} = a;\), jo \({b^2} \ge 0;\;\ ) tātad formas izpausmes \({a^{\frac{m}{n}}}\), netiks ņemts vērā \(a < 0.\) Šajā algebriskajā izteiksmē: \({a^n}\) \(a \ ) sauc par bāzi, un \(n\) ir \({a^n}\) tiek saukts par \(a\) pakāpju\(\;n\) vai arī tiek saukts par \(a\) pakāpei \(n,\;\)se ievērot šādus likumus no eksponentiem:

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\)	\({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\left( {ab} \right)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) katram \(a \ne 0\)

Eksponenciālajai funkcijai ir šāda forma:

\(f\left(x\right) = {a^x}\)

kur \(a > 0\) ir konstante un neatkarīgais mainīgais ir eksponents \(x\).

Lai veiktu eksponenciālās funkcijas analīzi, mēs apsvērsim trīs gadījumus

1. gadījums, kad bāze \(a = 1.\)

Šajā gadījumā \(a = 1,\) funkcija \(f\left( x \right) = {a^x}\) ir nemainīga funkcija.

2. gadījums, kad bāze \(a > 1\)

Šajā gadījumā mums ir šādas iespējas:

\(x\) vērtība
\(x < 0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x} < a\)
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(a < {a^x}\)

Funkcija \(f\left( x \right) = {a^x}\) ir stingri augoša funkcija, tas ir, ja \({x_2} > {x_1}\), tad:

\({a^{{x_2}}} > a_{}^{{x_2}}\)

\(f\left( {{x_2}} \right) > f\left( {{x_1}} \right)\)

Kad parādība tiek modelēta ar eksponenciālu funkciju ar \(a > 1\), mēs sakām, ka tā nodrošina eksponenciālu izaugsmi.

2. gadījums, kad bāze \(a < 1\).

\(x\) vērtība
\(x < 0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x} < a < 1\)

Ja \(a < 1\), funkcija \(f\left( x \right) = {a^x}\) ir stingri dilstoša funkcija, tas ir, ja \({x_2} > {x_1}\ ), tātad:

\({a^{{x_2}}} < a_{}^{{x_1}}\) \(f\left( {{x_2}} \right) < f\left( {{x_1}} \right) \) Kad parādība ir modeļiem ar eksponenciālu funkciju ar \(a < 1\), mēs sakām, ka tas rada samazināšanos vai samazināšanos eksponenciāls. Nākamajā diagrammā ir parādīta \({a^x}\) darbība trīs dažādos gadījumos.

Eksponenciālās funkcijas pielietojumi

1. piemērs Iedzīvotāju skaita pieaugums

Ar \({P_0}\) apzīmēsim sākotnējo populāciju un ar \(r \ge 0\) iedzīvotāju skaita pieauguma tempu, ja iedzīvotāju skaits laika gaitā paliek nemainīgs; funkcija

\(P\left(t \right) = {P_0}{\left({1 + r} \right)^t};\)

Atrast iedzīvotāju skaitu laikā t.

Praktisks piemērs 1

Meksikas iedzīvotāju skaits 2021. gadā ir 126 miljoni, un tas uzrādīja gada pieaugumu par 1,1%. Ja šis pieaugums tiks saglabāts, kāds būs iedzīvotāju skaits Meksikā 2031. gadā, gadā 2021?

Risinājums

Šajā gadījumā \({P_o} = 126\) un \(r = \frac{{1.1}}{{100}} = 0,011\), tāpēc jums vajadzētu izmantot:

\(P\left(t \right) = {P_0}{\left({1 + .0011} \right)^t}\)

Nākamajā tabulā parādīti rezultāti

gads	pagājušais laiks (\(t\))	Aprēķins	Iedzīvotāji (miljoni)
2021	0	\(P\left(t \right) = 126{\left({1,0011} \right)^0}\)	126
2031	10	\(P\left(t \right) = 126{\left({1,0011} \right)^{10}}\)	140.57
2051	30	\(P\left(t \right) = 126{\left({1,0011} \right)^{30}}\)	174.95

2. piemērs Salikto procentu aprēķināšana

Bankas piedāvā gada procentu likmi, bet reālā likme ir atkarīga no tā, cik mēnešus jūs to ieguldāt; Piemēram, ja jums tiek piedāvāta gada procentu likme r%, reālā mēneša likme ir \(\frac{r}{{12}}\)%, tad divu mēnešu likme ir \(\frac{r}{6}\)%, ceturksnis ir \(\frac{r}{4}\)%, ceturksnis ir \(\frac{r}{3}\)%, un semestris ir \(\frac{r}{2}\)%.

Praktiskais piemērs 2

Pieņemsim, ka jūs ieguldāt 10 000 bankā, un tā jums piedāvā šādas gada procentu likmes:

Termiņnoguldījumi	Gada likme	periodi gadā	faktiskā likme	Uzkrātā nauda \(k\) mēnešos
divus mēnešus	0.55%	6	\(\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}\)	\(10000{\left( {1 + 0,00091667} \right)^{\frac{k}{2}}}\)
trīs mēneši	1.87%	4	\(\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}\)	\(10000{\left( {1 + 0,00461667} \right)^{\frac{k}{3}}}\)
seši mēneši	1.56%	2	\(\frac{{1,56\% }}{4} = 0,78{\rm{\% }}\)	\(10000{\left( {1 + 0,0078} \right)^{\frac{k}{6}}}\)

Skaitlis \(e\), Eilera pastāvīgā un nepārtrauktā interese.

Tagad pieņemsim, ka mums ir sākuma kapitāls \(C\) un mēs to ieguldām ar fiksētu likmi \(r > 0\), un mēs sadalām gadu \(n\) periodos; gadā uzkrātais kapitāls ir vienāds ar:

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)

Lai analizētu, kā uzkrātais kapitāls uzvedas, kad \(n\), pieaug, mēs pārrakstīsim uzkrāto kapitālu viena gada laikā:

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)\(A = \;C{\left( {1 + \frac{1} {{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right) r}},\)

veicot \(m = \frac{n}{r}\), iegūstam:

\(A = C{\left( {1 + \frac{1}{m}} \right)^{mr}}\)\(A = C{\left( {{{\left( {1 + \) frac{1}{m}} \right)}^m}} \right)^r}.\)

Pieaugot \(n\), pieaug arī \(m = \frac{n}{r}.\)

Palielinoties \(m = \frac{n}{r},\), izteiksme \({\left( {1 + \frac{1}{m}} \right)^m}\) tuvojas tam, ko sauc par Eilera konstante vai skaitlis:

\(e \aptuveni 2,718281828 \lpunkti .\)

Eilera konstantei nav ierobežotas vai periodiskas decimālās izteiksmes.

Mums ir šādi tuvinājumi

\(C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \apmēram C{e^r},\) \(C{\left( {1 + \frac{r}{n}} \right)^{ns}} \apmēram C{e^{rs}}.\)

Uz izteicienu:

\(A = \;C{e^r},\)

Mēs to varam interpretēt divos veidos:

1.- Kā maksimālā summa, ko varam uzkrāt gadā, ieguldot kapitālu \(C,\;\) ar gada likmi \(r.\)

2.- Kā summa, ko mēs uzkrātu gadā, ja mūsu kapitāls tiktu nepārtraukti reinvestēts ar gada likmi \(r.\)

\(T\left(s \right) = \;C{e^{rs}},\)

ir uzkrātā summa, ja \(s\) gadi tiek ieguldīti ar nepārtrauktiem procentiem.

Konkrēts piemērs 3

Tagad atgriezīsimies pie konkrētā 2. piemēra daļas, kur gada likme ir 0,55% divos mēnešos. Aprēķiniet kapitālu, kas uzkrājas, ja sākumkapitāls ir 10 000 un reinvestē pusgadu, divus gadus, 28 mēnešus.

\(10{\left( {1,00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525\)

kā parādīts zemāk esošajā tabulā, \(m = \frac{n}{r},\) vērtība nav “maza”, un augstāk esošā tabula norāda, ka \({\left( {1 + \frac{1}{ m}} \right)^m}\) ir tuvu Eilera konstantei.

Laiks	Periodu skaits (\(k\))	Uzkrātais kapitāls, tūkstošos, reinvestēts ik pēc diviem mēnešiem
Pus gads	3	\(10{\left( {1,00091667} \right)^3} = 10.{\rm{\;}}027525\)
Divus gadus	12	\(10{\left( {1,00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 mēneši	19	\(10{\left( {1,00091667} \right)^{19}} = 10.\;175612\)

Laiks	Gadu laiks (\(s\))	Uzkrātais kapitāls, tūkstošos, ieguldīt ar nepārtrauktiem procentiem
Pus gads	\(s = \frac{1}{2}\)	\(10{e^{0,0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\)
Divus gadus	\(s = 2\)	\(10{\left( {1,00091667} \right)^{0,0055\left( 2 \right)}} = 10110.{\rm{\;}}607\)
38 mēneši	\(s = \frac{{19}}{6}\)	\(10{\left( {1,00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

2. piemērs Nolietojums

Praktisks piemērs 1

Dators katru gadu nolietojas par 30%, ja dators maksā 20 000 peso, nosakiet datora cenu par \(t = 1,12,\;14,\;38\) mēnešiem.

Šajā gadījumā vienam ir:

\(P\left(t \right) = 20000{\rm{\;}}{\left({1–0,30} \right)^t}\)

Ar \(t\) gados, aizstājot \(t\) nākamajā tabulā, tiek iegūts

laiks mēnešos	laiks gados	aprēķinus	Skaitliskā vērtība
1	\(\frac{1}{{12}}\)	\(P\left(t \right) = 20000{\rm{\;}}{\left( {1–.30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left(t \right) = 20000{\rm{\;}}{\left( {1–0,30} \right)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left(t \right) = 20000{\rm{\;}}{\left({1–.30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left(t \right) = 20000{\rm{\;}}{\left({1–.30} \right)^{\frac{7}{6}}}\)	6464.0859