Definicja funkcji wykładniczej

Funkcja wykładnicza modeluje różne zjawiska naturalne oraz sytuacje społeczne i gospodarcze, dlatego tak ważne jest identyfikowanie funkcji wykładniczych w różnych kontekstach.

Pamiętajmy, że dla liczby \({a^1} = a,{a^2} = aa,\;{a^3} = aaa\) jest zdefiniowana, ogólnie mamy to dla dowolnego \(n\ ) liczba naturalna:

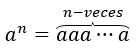
W przypadku \(a \ne 0\) mamy, że: \({a^0} = 1,\;\) w rzeczywistości, gdy \(a \ne 0,\) ma sens wykonanie operacji \ (\frac{a}{a} = 1;\) stosując prawo wykładników mamy:

\(\frac{a}{a} = 1\)

\({a^{1 – 1}} = 1\)

\({a^0} = 1.\)

Gdy \(a = 0\), poprzednie rozumowanie nie ma sensu, dlatego wyrażenie \({0^0},\) nie ma matematycznej interpretacji.

W przypadku, gdy \(b > 0\) i jest prawdą, że \({b^n} = a,\) mówi się, że \(b\) jest n-tym pierwiastkiem z \(a\) i zwykle oznaczane jako \ (b = {a^{\frac{1}{n}}},\;\) lub \(b = \sqrt[n]{a}\).

Gdy \(a < 0\), nie ma liczby rzeczywistej \(b\) takiej, że \({b^2} = a;\) ponieważ \({b^2} \ge 0;\;\ ) więc wyrażenia postaci \({a^{\frac{m}{n}}}\), nie będzie brane pod uwagę dla \(a < 0.\) W następującym wyrażeniu algebraicznym: \({a^n}\) \(a \ ) nazywa się bazą, a \(n\) jest nazywany wykładnikiem, \({a^n}\)jest nazywany potęgą\(\;n\) \(a\) lub jest również nazywany \(a\) do potęgi \(n,\;\)se postępować zgodnie z poniższymi prawami wykładników:

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{a^m}}} = {a^{n – m}}\)	\({\lewo( {{a^n}} \prawo)^m} = {a^{nm}} = {\lewo( {{a^m}} \prawo)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\left( {ab} \right)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) dla każdego \(a \ne 0\)

Funkcja wykładnicza ma postać:

\(f\lewo( x \prawo) = {a^x}\)

gdzie \(a > 0\) jest stałą, a zmienną niezależną jest wykładnik \(x\).

Aby dokonać analizy funkcji wykładniczej, rozważymy trzy przypadki

Przypadek 1 Gdy podstawa \(a = 1.\)

W tym przypadku \(a = 1,\) funkcja \(f\left( x \right) = {a^x}\) jest funkcją stałą.

Przypadek 2 Gdy podstawa \(a > 1\)

W tym przypadku mamy:

Wartość \(x\)
\(x < 0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x} < a\)
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(a < {a^x}\)

Funkcja \(f\left( x \right) = {a^x}\) jest funkcją ściśle rosnącą, to znaczy, jeśli \({x_2} > {x_1}\), to:

\({a^{{x_2}}} > a_{}^{{x_2}}\)

\(f\lewo( {{x_2}} \prawo) > f\lewo( {{x_1}} \prawo)\)

Kiedy zjawisko jest modelowane za pomocą funkcji wykładniczej, gdzie \(a > 1\), mówimy, że przedstawia ono wzrost wykładniczy.

Przypadek 2 Gdy podstawa \(a < 1\).

Wartość \(x\)
\(x < 0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x} < a < 1\)

Gdy \(a < 1\), funkcja \(f\left( x \right) = {a^x}\) jest funkcją ściśle malejącą, to znaczy, jeśli \({x_2} > {x_1}\ ), Więc:

\({a^{{x_2}}} < a_{}^{{x_1}}\) \(f\left( {{x_2}} \right) < f\left( {{x_1}} \right) \) Kiedy zjawisko jest modele z funkcją wykładniczą, gdzie \(a < 1\), mówimy, że przedstawia ona zanik lub spadek wykładniczy. Poniższy wykres ilustruje zachowanie \({a^x}\) w trzech różnych przypadkach.

Zastosowania funkcji wykładniczej

Przykład 1 Wzrost populacji

Będziemy oznaczać przez \({P_0}\) początkową populację i przez \(r \ge 0\) tempo wzrostu populacji, jeśli współczynnik zaludnienia pozostaje stały w czasie; funkcja

\(P\lewo( t \prawo) = {P_0}{\lewo( {1 + r} \prawo)^t};\)

Znajdź populację w czasie t.

Praktyczny przykład 1

Populacja Meksyku w roku 2021 wynosi 126 milionów i wykazywała roczny wzrost o 1,1%, Jeśli ten wzrost się utrzyma, jaka populacja będzie w Meksyku w roku 2031, w roku 2021?

Rozwiązanie

W tym przypadku \({P_o} = 126\) i \(r = \frac{{1.1}}{{100}} = 0,011\), więc powinieneś użyć:

\(P\lewo( t \prawo) = {P_0}{\lewo( {1 + .0011} \prawo)^t}\)

Poniższa tabela przedstawia wyniki

Rok	upływający czas (\(T\))	Obliczenie	Populacja (miliony)
2021	0	\(P\lewo( t \prawo) = 126{\lewo( {1,0011} \prawo)^0}\)	126
2031	10	\(P\lewo( t \prawo) = 126{\lewo( {1,0011} \prawo)^{10}}\)	140.57
2051	30	\(P\lewo( t \prawo) = 126{\lewo( {1,0011} \prawo)^{30}}\)	174.95

Przykład 2 Obliczanie procentu składanego

Banki oferują roczną stopę procentową, ale rzeczywista stopa procentowa zależy od tego, ile miesięcy ją inwestujesz; Na przykład, jeśli zaoferowano Ci roczną stopę procentową r%, rzeczywista miesięczna stopa procentowa wynosi \(\frac{r}{{12}}\)%, dwumiesięczna stopa procentowa wynosi \(\frac{r}{6}\)%, kwartalnie to \(\frac{r}{4}\)%, kwartalnie to \(\frac{r}{3}\)%, a semestr to \(\frac{r}{2}\)%.

Praktyczny przykład 2

Załóżmy, że inwestujesz 10 000 w bank, który oferuje ci następujące roczne stopy procentowe:

Lokaty terminowe	Roczna stawka	okresy w roku	rzeczywista stawka	Zgromadzone pieniądze w \(k\) miesiącach
dwa miesiące	0.55%	6	\(\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}\)	\(10000{\left( {1 + 0,00091667} \right)^{\frac{k}{2}}}\)
trzy miesiące	1.87%	4	\(\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}\)	\(10000{\left( {1 + 0,00461667} \right)^{\frac{k}{3}}}\)
sześć miesięcy	1.56%	2	\(\frac{{1,56\% }}{4} = 0,78{\rm{\% }}\)	\(10000{\left( {1 + 0,0078} \right)^{\frac{k}{6}}}\)

Liczba \(e\), stałe i ciągłe zainteresowanie Eulera.

Załóżmy teraz, że mamy kapitał początkowy \(C\) i inwestujemy go po stałej stopie \(r > 0\) oraz dzielimy rok na \(n\) okresów; kapitał zgromadzony w ciągu roku jest równy:

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)

Aby przeanalizować, jak zachowuje się skumulowany kapitał, gdy \(n\), rośnie, przepiszemy skumulowany kapitał za rok:

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)\(A = \;C{\left( {1 + \frac{1} {{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right) r}},\)

robiąc \(m = \frac{n}{r}\), otrzymujemy:

\(A = C{\left( {1 + \frac{1}{m}} \right)^{mr}}\)\(A = C{\left( {{{\left( {1 + \ frac{1}{m}} \right)}^m}} \right)^r}.\)

Gdy \(n\) rośnie, rośnie też \(m = \frac{n}{r}.\)

Ponieważ \(m = \frac{n}{r},\) rośnie, wyrażenie \({\left( {1 + \frac{1}{m}} \right)^m}\)zbliża się do tzw. Stała lub liczba Eulera:

\(e \około 2,718281828 \ldots .\)

Stała Eulera nie ma skończonego ani okresowego wyrażenia dziesiętnego.

Mamy następujące przybliżenia

\(C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \około C{e^r},\) \(C{\left( {1 + \frac{r}{n}} \right)^{ns}} \około C{e^{rs}}.\)

Do wyrażenia:

\(A = \;C{e^r},\)

Możemy to zinterpretować na dwa sposoby:

1.- Jako maksymalną kwotę, jaką możemy zgromadzić w ciągu roku, gdy inwestujemy kapitał \(C,\;\) według rocznej stopy \(r.\)

2.- Jako kwotę, którą zgromadzilibyśmy w ciągu roku, gdyby nasz kapitał był stale reinwestowany według rocznej stopy \(r.\)

\(T\left( s \right) = \;C{e^{rs}},\)

to kwota zgromadzona, jeśli \(s\) lat są inwestowane z ciągłym oprocentowaniem.

Konkretny przykład 3

Teraz wrócimy do fragmentu konkretnego przykładu 2, gdzie roczna stopa wynosi 0,55% w ratach dwumiesięcznych. Oblicz kapitał, który się gromadzi, jeśli kapitał założycielski wynosi 10 000 i reinwestuje przez pół roku, dwa lata i 28 miesięcy.

\(10{\left( {1.00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525\)

jak pokazuje poniższa tabela, wartość \(m = \frac{n}{r},\) nie jest „mała”, a powyższa tabela wskazuje, że \({\left( {1 + \frac{1}{ m}} \right)^m}\) jest bliskie stałej Eulera.

Czas	Liczba okresów (\(k\))	Zgromadzony kapitał, w tysiącach, reinwestowany co dwa miesiące
pół roku	3	\(10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525\)
Dwa lata	12	\(10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 miesięcy	19	\(10{\lewo( {1.00091667}\prawo)^{19}} = 10.\;175612\)

Czas	Pora lat (\(s\))	Zgromadzony kapitał, w tysiącach, inwestuje z ciągłym oprocentowaniem
pół roku	\(s = \frac{1}{2}\)	\(10{e^{0,0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\)
Dwa lata	\(s = 2\)	\(10{\lewo( {1,00091667} \prawo)^{0,0055\lewo( 2 \prawo)}} = 10110.{\rm{\;}}607\)
38 miesięcy	\(s = \frac{{19}}{6}\)	\(10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

Przykład 2 Amortyzacja

Praktyczny przykład 1

Komputer traci na wartości 30% każdego roku, jeśli komputer kosztował 20 000 pesos, ustal cenę komputera na \(t = 1,12,\;14,\;38\) miesięcy.

W tym przypadku jeden ma:

\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0,30} \right)^t}\)

Z \(t\) w latach, podstawienie \(t\) w poniższej tabeli daje

czas w miesiącach	czas w latach	obliczenia	Wartość numeryczna
1	\(\frac{1}{{12}}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	6464.0859