Exponentiell funktionsdefinition

Hämning Strängteorin / by admin / April 02, 2023

Marco Antonio Rodriguez Andrade
Master of Mathematics, Dr of Science

Exponentialfunktionen modellerar olika naturfenomen och sociala och ekonomiska situationer, varför det är viktigt att identifiera exponentiella funktioner i olika sammanhang.

Låt oss komma ihåg att för ett tal är ${a^1} = a,{a^2} = aa,\;{a^3} = aaa$ definierat, i allmänhet har vi det för alla \(n\ ) nummer naturligt:

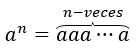
I fallet $a \ne 0$, har vi det: ${a^0} = 1,\;$ i själva verket, när $en \ne 0,$ är det vettigt att göra operationen \ (\frac{a}{a} = 1;\) när vi tillämpar exponentlagen har vi:

$\frac{a}{a} = 1$

${a^{1 – 1}} = 1$

${a^0} = 1.$

När $a = 0$ är det tidigare resonemanget inte vettigt, därför saknar uttrycket ${0^0},$ en matematisk tolkning.

I händelse av att $b > 0$ och det är sant att ${b^n} = a,$ sägs det att $b$ är den n: te roten av $a$ och är vanligtvis betecknas som \ (b = {a^{\frac{1}{n}}},\;\) eller $b = \sqrt[n]{a}$.

När $a < 0$, finns det inget reellt tal $b$ så att ${b^2} = a;$ eftersom ${b^2} \ge 0;\;\ ) så formens uttryck \({a^{\frac{m}{n}}}$, kommer inte att beaktas för $a < 0.$ I följande algebraiska uttryck: ${a^n}$ $a \ ) kallas bas, och \(n$ är kallas exponent, ${a^n}$ kallas potensen$\;n$ av $a$ eller kallas även $a$ till potensen $n,\;$se följa följande lagar av exponenterna:

instagram story viewer

${a^n}{a^m} = {a^{n + m}}$	$\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}$	${\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}$
$\frac{1}{{{a^n}}} = {a^{ – n}}$	${a^n} = \frac{1}{{{a^{ – n}}}}$	${\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}$
${\left( {ab} \right)^n} = {a^n}{b^n}$	${\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}$	${a^0} = 1$ för varje $a \ne 0$

Exponentialfunktionen har formen:

$f\left( x \right) = {a^x}$

där $a > 0$ är en konstant och den oberoende variabeln är exponenten $x$.

För att göra en analys av exponentialfunktionen kommer vi att överväga tre fall

Fall 1 När basen $a = 1.$

I detta fall är $a = 1,$ funktionen $f\left( x \right) = {a^x}$ en konstant funktion.

Fall 2 När grunden $a > 1$

I det här fallet har vi följande:

Värdet av $x$
$x < 0$	$0 < {a^x} < 1$
$x = 0$	${a^0} = 1$
$0 < x < 1$	$1 < {a^x} < a$
$x = 1$	${a^x} = 1$
$x > 1$	$a < {a^x}$

Funktionen $f\left( x \right) = {a^x}$ är en strikt ökande funktion, det vill säga om ${x_2} > {x_1}$, då:

${a^{{x_2}}} > a_{}^{{x_2}}$

$f\left( {{x_2}} \right) > f\left( {{x_1}} \right)$

När ett fenomen modelleras med en exponentiell funktion, med $a > 1$, säger vi att det presenterar exponentiell tillväxt.

Fall 2 När grunden $a < 1$.

Värdet av $x$
$x < 0$	${a^x} > 1$
$x = 0$	${a^0} = 1$
$0 < x < 1$	$0 < {a^x} < 1$
$x = 0$	${a^x} = 1$
$x > 1$	$0 < {a^x} < a < 1$

När $a < 1$, är funktionen $f\left( x \right) = {a^x}$ en strikt minskande funktion, det vill säga om \({x_2} > {x_1}\ ), alltså:

${a^{{x_2}}} < a_{}^{{x_1}}$ $f\left( {{x_2}} \right) < f\left( {{x_1}} \right) $ När ett fenomen är modeller med en exponentiell funktion, med $a < 1$, säger vi att den presenterar en avklingning eller minskning exponentiell. Följande graf illustrerar beteendet hos ${a^x}$, i dess tre olika fall.

Tillämpningar av exponentialfunktionen

Exempel 1 Befolkningstillväxt

Vi kommer att beteckna med ${P_0}$ den initiala populationen och med $r \ge 0$ befolkningstillväxthastigheten, om befolkningshastigheten förblir konstant över tiden; funktionen

$P\left( t \right) = {P_0}{\left( {1 + r} \right)^t};$

Hitta populationen vid tidpunkten t.

Praktiskt exempel 1

Mexikos befolkning år 2021 är 126 miljoner och uppvisade en årlig tillväxt på 1,1%, Om denna tillväxt bibehålls, vilken befolkning kommer det att finnas i Mexiko år 2031, år 2021?

Lösning

I det här fallet ${P_o} = 126$ och $r = \frac{{1.1}}{{100}} = 0,011$, så bör du använda:

$P\left( t \right) = {P_0}{\left( {1 + .0011} \right)^t}$

Följande tabell visar resultaten

År	förfluten tid ($t$)	Beräkning	Befolkning (miljoner)
2021	0	$P\left( t \right) = 126{\left( {1.0011} \right)^0}$	126
2031	10	$P\left( t \right) = 126{\left( {1.0011} \right)^{10}}$	140.57
2051	30	$P\left( t \right) = 126{\left( {1.0011} \right)^{30}}$	174.95

Exempel 2 Beräkning av ränta

Banker erbjuder en årlig ränta, men den reala räntan beror på hur många månader du investerar den; Om du till exempel erbjuds en årlig ränta på r%, är den reala månadsräntan $\frac{r}{{12}}$%, den varannan månadsräntan är $\frac{r}{6}$%, kvartalsvis är $\frac{r}{4}$%, kvartalsvis är $\frac{r}{3}$%, och terminen är $\frac{r}{2}$%.

Praktiskt exempel 2

Anta att du investerar 10 000 i en bank och de erbjuder dig följande årliga räntor:

Tidsbegränsad inlåning	Årlig ränta	perioder på ett år	faktisk kurs	Ackumulerade pengar på $k$ månader
två månader	0.55%	6	$\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}$	$10000{\left( {1 + 0,00091667} \right)^{\frac{k}{2}}}$
tre månader	1.87%	4	$\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}$	$10000{\left( {1 + 0,00461667} \right)^{\frac{k}{3}}}$
sex månader	1.56%	2	$\frac{{1,56\% }}{4} = 0,78{\rm{\% }}$	$10000{\left( {1 + 0,0078} \right)^{\frac{k}{6}}}$

Talet $e$, Eulers konstanta och kontinuerliga intresse.

Anta nu att vi har ett startkapital $C$ och vi investerar det till en fast ränta $r > 0$, och vi delar upp året i $n$ perioder; det ackumulerade kapitalet under ett år är lika med:

$A = \;C{\left( {1 + \frac{r}{n}} \right)^n}$

För att analysera hur det ackumulerade kapitalet beter sig när $n$, växer, kommer vi att skriva om det ackumulerade kapitalet, på ett år:

$A = \;C{\left( {1 + \frac{r}{n}} \right)^n}$$A = \;C{\left( {1 + \frac{1} {{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right) r}},$

genom att göra $m = \frac{n}{r}$, får vi:

$A = C{\left( {1 + \frac{1}{m}} \right)^{mr}}$$A = C{\left( {{{\left( {1 + \ frac{1}{m}} \right)}^m}} \right)^r}.$

När $n$ växer, växer också $m = \frac{n}{r}.$

När $m = \frac{n}{r},$ växer, närmar sig uttrycket ${\left( {1 + \frac{1}{m}} \right)^m}$ det som kallas Euler konstant eller tal:

$e \ca 2,718281828 \ldots .$

Eulers konstant har inte ett ändligt eller periodiskt decimaluttryck.

Vi har följande uppskattningar

$C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \approx C{e^r},$ $C{\left( {1 + \frac{r}{n}} \right)^{ns}} \approx C{e^{rs}}.$

Till uttrycket:

$A = \;C{e^r},$

Vi kan tolka det på två sätt:

1.- Som det maximala belopp som vi kan ackumulera under ett år när vi investerar kapital $C,\;$ i en årlig takt $r.$

2.- Som det belopp som vi skulle ackumulera under ett år om vårt kapital kontinuerligt återinvesterades i en årlig takt $r.$

$T\left( s \right) = \;C{e^{rs}},$

är det belopp som ackumuleras om $s$ år investeras med löpande ränta.

Konkret exempel 3

Nu ska vi återkomma till en del av konkret exempel 2, där den årliga räntan är 0,55 % i delbetalningar varannan månad. Beräkna kapitalet som ackumuleras om startkapitalet är 10 000 och återinvesterar ett halvår, två år, 28 månader.

$10{\left( {1.00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525$

som tabellen nedan visar är värdet för $m = \frac{n}{r},$ inte "litet" och tabellen ovan indikerar att ${\left( {1 + \frac{1}{ m}} \right)^m}$ är nära Eulers konstant.

Tid	Antal perioder ($k$)	Ackumulerat kapital, i tusental, återinvesterat varannan månad
Halvår	3	$10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525$
Två år	12	$10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557$
38 månader	19	$10{\left( {1.00091667} \right)^{19}} = 10.\;175612$

Tid	Tid på år ($s$)	Ackumulerat kapital, i tusental, investera med kontinuerlig ränta
Halvår	$s = \frac{1}{2}$	$10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538$
Två år	$s = 2$	$10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607$
38 månader	$s = \frac{{19}}{6}$	$10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692$

Exempel 2 Avskrivningar

Praktiskt exempel 1

En dator sjunker med 30 % varje år, om en dator kostar $20 000 pesos, bestäm priset på datorn för $t = 1,12,\;14,\;38$ månader.

I det här fallet har man:

$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0,30} \right)^t}$

Med $t$ i år, ersätter $t$ i följande tabell

tid i månader	tid i år	beräkningar	Numeriskt värde
1	$\frac{1}{{12}}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}$	19414.289
12	1	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}$	14000
14	$\frac{7}{6}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}$	13192.012
38	$\frac{{19}}{6}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}$	6464.0859

Taggar moln

Betyg

Visningar

Kommentarer

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\)	\({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\left( {ab} \right)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) för varje \(a \ne 0\)

Värdet av \(x\)
\(x < 0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x} < a\)
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(a < {a^x}\)

Värdet av \(x\)
\(x < 0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x} < a < 1\)

Tid	Tid på år (\(s\))	Ackumulerat kapital, i tusental, investera med kontinuerlig ränta
Halvår	\(s = \frac{1}{2}\)	\(10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\)
Två år	\(s = 2\)	\(10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607\)
38 månader	\(s = \frac{{19}}{6}\)	\(10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

År	förfluten tid (\(t\))	Beräkning	Befolkning (miljoner)
2021	0	\(P\left( t \right) = 126{\left( {1.0011} \right)^0}\)	126
2031	10	\(P\left( t \right) = 126{\left( {1.0011} \right)^{10}}\)	140.57
2051	30	\(P\left( t \right) = 126{\left( {1.0011} \right)^{30}}\)	174.95

Tidsbegränsad inlåning	Årlig ränta	perioder på ett år	faktisk kurs	Ackumulerade pengar på \(k\) månader
två månader	0.55%	6	\(\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}\)	\(10000{\left( {1 + 0,00091667} \right)^{\frac{k}{2}}}\)
tre månader	1.87%	4	\(\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}\)	\(10000{\left( {1 + 0,00461667} \right)^{\frac{k}{3}}}\)
sex månader	1.56%	2	\(\frac{{1,56\% }}{4} = 0,78{\rm{\% }}\)	\(10000{\left( {1 + 0,0078} \right)^{\frac{k}{6}}}\)

Tid	Antal perioder (\(k\))	Ackumulerat kapital, i tusental, återinvesterat varannan månad
Halvår	3	\(10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525\)
Två år	12	\(10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 månader	19	\(10{\left( {1.00091667} \right)^{19}} = 10.\;175612\)

tid i månader	tid i år	beräkningar	Numeriskt värde
1	\(\frac{1}{{12}}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	6464.0859