Definition of Pythagorean Theorem

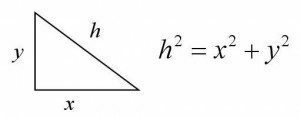It is calledtheoremTo that proposition that is plausible to be proved in a way logic and starting from a axiom, or failing that, other theorems already provenmeanwhile, it turns out to be necessary to observe certain rules of inference to get the aforementioned demonstration.

On your side, Pythagoras of Samos was a popular philosopher and mathematician greek who lived in Greece between the years 582 and 507 B.C. Although it bears his name in honor of him for having given the necessary conditions for him to finally find a demonstration, the Pythagoras' theorem was not created directly by Pythagoras but was actually developed and applied a long time before both in Babylon as in India, although, it was the school of Pythagoras which managed to find a formal and forceful answer regarding the theorem.

Meanwhile, the aforementioned theorem holds that in a triangle rectangle, the square of the hypotenuse is equal to the sum of the squares of the legs. To better understand the issue, it is necessary to take into account that a right triangle is one that has a right angle that measures 90 °, then that the hypotenuse is that side of the triangle that has a greater length and that is directly opposite to the right angle and finally that the legs are the two smaller sides of the triangle right.

It should be noted that the theorem that concerns us is the one with the greatest number of proofs and they were achieved using very different methods.

In the twentieth century, more precisely in the year 1927, a mathematician, E.S. Loomis compiled more than 350 proofs of the Pythagorean theorem, a situation that brought a little more order to the subject,, they were classified into four groups: geometric proofs (they are made based on the comparison of the areas), algebraic proofs (developed based on the relationship between the sides and the segments of the triangle) dynamic demonstrations (they invoke the properties of the force) Y quaternionic proofs (They appear by the use of vectors).