What is the Hierarchy of Operations?

The hierarchy of operations is a mathematical convention that establishes the order in which combined calculation actions should be performed in the same mathematical statement, that is, when there is a mathematical statement where there are mathematical operations (addition, subtraction, multiplication, division, powers, and roots) combined, these have to be done in a specific order to arrive at a result common.

But why is a hierarchy needed? In order to answer it, we first have to understand well the nature of mathematical operations, which consists of a transformation that is applied to the elements of a set. Let us think, for example, of the set of real numbers, that is, those numbers that we all know. If we take a number a and add it with another number b we will obtain another number c that belongs to the same set of real numbers, that is:

a+b = c

In addition, the order in which the addends are presented does not affect the final result, that is, that

a+b = b+a, this property is called commutativity. It is important to talk about addition because it is the basic operation from which all the others are derived. A multiplication is nothing more than a series of repeated additions. If we have a number a again and we multiply it by a number b, what we are doing is sometimes adding the number b with itself, or, alternatively, adding b times the number a with itself. The latter is so since multiplication is commutative like addition, this implies that: a⋅b = b⋅a. The aforementioned can be expressed as: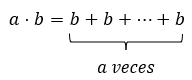

We can easily visualize this with an example. Let's do the 5×2 multiplication:

5×2 = 2×5 = 2+2+2+2+2 = 5+5 = 10

Now, what if we have to perform an operation where we have combined addition with multiplication? For example: a⋅b+c. What is the order in which addition and multiplication must be performed? Which operation do we have to give preference to? If we perform the multiplication first and develop it as a sum we would have:

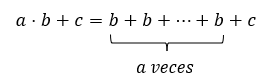
Now, if we performed the addition first and then the multiplication we would get:

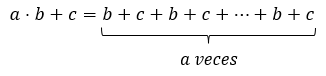
Since addition is commutative we can regroup the right hand side of the equation to get:

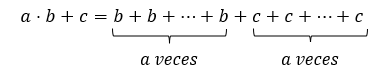
Comparing the results obtained in both situations it is easy to realize that:

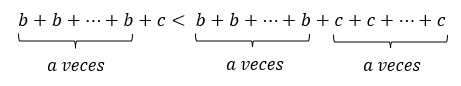
We conclude then that the order in which it is decided to carry out the operations affects the result obtained. The same happens when we involve powers. When we raise a number b to a power c, what we are doing is multiplying c times the number b with itself, that is:

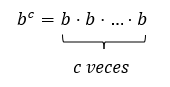
We now proceed to perform the following combined operation involving multiplication and power a⋅b^c in a different order as we did in the previous case. If we first give priority to power we have:

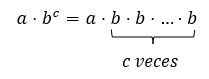
Now, if we perform the multiplication first and then the power, we would have:

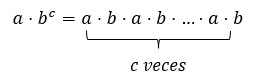
Taking advantage of the commutativity of multiplication we can regroup the right hand side of the equation as:

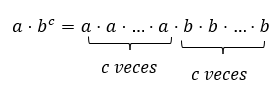
Again, we can compare the results obtained by performing the operations in a different order to realize that:

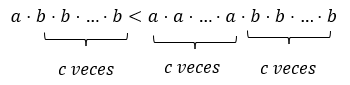
Also in this case the order in which the operations are performed affects the result obtained. So, what is the order in which the operations have to be performed? The hierarchy of operations establishes that powers are at a higher level of hierarchy than multiplications, in such a way that powers have precedence in a mathematical statement. In turn, multiplications have a higher hierarchy level than additions.

But what about subtraction, division, and roots? Subtraction is the opposite operation of addition, when we subtract a number b from a number a we obtain another number c such that c+b=a. Something similar happens with division and subtraction. If we divide a number a by a number b and get a number c as a result, we have found a number such that b⋅c=a. And finally, by calculating the root b of a number a we find a number c such that c^b=a. These equivalences put subtraction, division, and root on the same hierarchy level as addition, multiplication, and power, respectively.

Parentheses and brackets practices

Now, what happens if we want to give priority to some operations in a mathematical statement regardless of their hierarchy level? To do this, parentheses and square brackets are used. Suppose we have the statement of the principle a⋅b+c. With what we have said before we already know that we have to perform the multiplication first and then the addition. But, what if we wanted this not to be the case? To do this, we would have to use parentheses or square brackets to separate the addition from the multiplication and thus give priority to calculating the addition first, that is: a⋅(b+c). This causes statements separated by parentheses and square brackets to have the highest priority over all other operations.

With everything said above, the hierarchy of operations, or the order in which they must be carried out, is as follows:

1) Parentheses and brackets
2) Powers and roots
3) Multiplications and divisions
4) Addition and subtraction

References

h. Behnke, F. Bachman, K. Fladt, W. Suss, H. Gerike, F. Hohenberg, G. Pickert, H. Rau & S. h. Gould. (1983). Fundamentals of Mathematics: Volume I. Cambridge, Massachusetts and London: The MIT Press.