Definition of Mixed, Unit, Homogeneous and Heterogeneous Fractions

Mixed. A mixed fraction is made up of an integer greater than or equal to one and a proper fraction, the general spelling of a fraction mixed is of the form: \(a + \frac{c}{d},\) whose compact writing is: \(a\frac{c}{d},\;\), that is: \(a\ fraction{c}{d} = a + \frac{c}{d}\). The number \(a\) is called the integer part of the mixed fraction and \(\frac{c}{d}\) is called its fractional part.

homogeneous. If two or more fractions have the same denominator, they are said to be like fractions. For example, the fractions \(\frac{3}{4},\) \(\frac{7}{4},\) \(\frac{1}{4},\) \(\frac{{ 10}}{4}\) are homogeneous because they all have the same denominator, which in this case is \(4\). While the fractions \(\frac{3}{4},\) \(\frac{7}{4},\) \(\frac{1}{4},\) \(\frac{5} {2}\) are not homogeneous fractions since the denominator of \(\frac{5}{2}\) is \(2\) and the denominator of the other fractions is \(4\). One of the advantages of the homogeneous fractions is that the arithmetic operations of addition and subtraction of functions is very simple.

heterogeneous. If two or more fractions at least two of them do not have the same denominator then these fractions are said to be heterogeneous fractions. The following fractions are heterogeneous: \(\frac{3}{5},\;\) \(\frac{7}{5}\), \(\frac{1}{4},\) \(\ frac{2}{5}\).

unitary. A fraction is identified as a unit if the numerator is equal to 1 \(1,\) \(2\). The following fractions are examples of unit fractions: \(\frac{1}{2},\;\) \(\frac{1}{3}\), \(\frac{1}{4}\), \(\;\frac{1}{5}\).

Verbal expression of a mixed fraction

mixed fraction	Verbal expression
\(3\frac{1}{2} = \)	Three and a half whole
\(5\frac{3}{4} = \)	Five integers and three quarters
\(10\frac{1}{8} = \)	Ten integers with an eighth

Converting a mixed fraction to an improper fraction

Mixed fractions are useful for estimation, for example, it is easy to establish:

\(5\frac{1}{{20}} > 4\frac{9}{{10}}\)

However, mixed fractions are usually impractical to perform operations such as multiplication and division, which is why it is important how to convert to a mixed fraction.

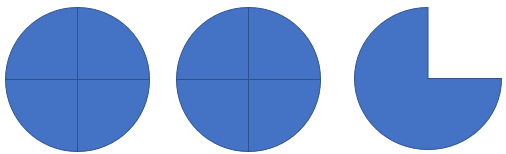
The previous figure represents the mixed fraction \(2\frac{3}{4}\), now each integer is composed of four quarters, so in 2 integers there are 8 quarters and to these we must add the other 3 quarters, that is say:

\(2\frac{3}{4} = \frac{{2\left( 4 \right) + 3}}{4} = \frac{{11}}{4}\)

Generally:

\(a\frac{c}{d} = \frac{{ad + c}}{d}\)

The following table shows other examples.

mixed fraction	Operations to perform	improper fraction
\(3\frac{1}{2}\)	\(\frac{{3\left( 2 \right) + 1}}{2}\)	\(\frac{7}{2}\)
\(5\frac{3}{4}\)	\(\frac{{5\left( 4 \right) + 3}}{4}\)	\(\frac{{23}}{4}\)
\(10\frac{1}{8}\)	\(\frac{{10\left( 8 \right) + 1}}{8}\)	\(\frac{{81}}{8}\)

Converting an Improper Fraction to a Mixed Fraction

To convert an improper fraction to a mixed fraction, calculate the quotient and the remainder of dividing the numerator by the denominator. The quotient obtained will be the integer part of the mixed fraction and the proper fraction will be \(\frac{{{\rm{remainder}}}}{{{\rm{denominator}}}}\)

Example

To convert \(\frac{{25}}{7}\) to a mixed fraction:

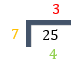
For the operations carried out we obtain:

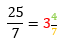
The table below shows other examples.

improper fraction	Calculation of the quotient and the remainder	improper fraction
\(\frac{{25}}{7}\)		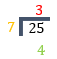\(3\frac{4}{7}\)
\(\frac{{35}}{8}\)		\(4\frac{3}{8}\)
\(\frac{{46}}{5}\)		\(9\frac{1}{5}\)

Everyday use of mixed and proper fractions

In everyday life we ​​need to measure, buy, compare prices, offer discounts; To measure we need units of measure and they do not always offer whole units of the products and you do not always pay with a whole quantity of coins for a unit.

For example, it is common for certain liquids to be sold in containers whose contents are \(\frac{3}{4}\;\) of a liter, half a gallon, or a gallon and a half. Maybe when you go to buy a tube you ask for \(\frac{1}{8},\;\) \(\frac{7}{8},{\rm{\;}}\) \({\rm {3}}\frac{1}{2}\) and you don't need to say the unit of measurement, which in this case is the inch.

Basic operations of like fractions

The sum of \(\frac{3}{4}\) and \(\frac{2}{4}\), is exemplified in the following scheme:

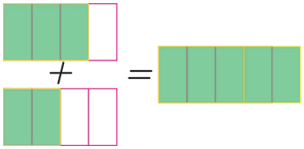
\(\frac{3}{4} + \frac{2}{4} = \frac{{3 + 2}}{4} = \frac{5}{4}\)

While the subtraction is done as follows:

\(\frac{3}{4} – \frac{2}{4} = \frac{{3 – 2}}{4} = \frac{1}{4}\)

In general, for homogeneous fractions:

\(\frac{a}{d} + \frac{b}{d} = \frac{{a + b}}{d}\)

\(\frac{a}{d} – \frac{b}{d} = \frac{{a – b}}{d}\)

The Egyptians and unit fractions

The Egyptian culture achieved a remarkable technological development and this would not have happened without a development on a par with mathematics. There are historical vestiges where you can find records of the use of fractions in Egyptian culture, with a particularity, they only used unitary fractions.

There are several cases where writing a fraction as a sum of unit fractions is as simple as

\(\frac{3}{n} = \frac{1}{n} + \frac{1}{{2n}}\)

In the case that \(n = 2q + 1\), that is to say odd, we have that:

\(\frac{2}{n} = \frac{1}{{q + 1}} + \frac{1}{{n\left( {q + 1} \right)}}\)

We will illustrate this with two examples.

To express \(\frac{2}{{11}}\); in this case we have \(11 = 2\left( 5 \right) + 1\), therefore:

\(\frac{2}{{11}} = \frac{1}{6} + \frac{1}{{11\left( 6 \right)}},\)

that is to say,

\(\frac{2}{{11}} = \frac{1}{6} + \frac{1}{{66}}\)

To express \(\frac{2}{{17}}\); in this case we have \(17 = 2\left( 8 \right) + 1\),

\(\frac{2}{{15}} = \frac{1}{8} + \frac{1}{{120}}\)

Next, we show some fractions as sum of unit fractions,

Fraction	Expression as sum of unit fractions	Fraction	Expression as sum of unit fractions
\(\frac{3}{n}\)	\(\frac{1}{n} + \frac{1}{{2n}}\)	\(\frac{5}{8}\)	\(\frac{1}{2} + \frac{1}{8}\)
\(\frac{2}{3}\)	\(\frac{1}{2} + \frac{1}{6}\)	\(\frac{7}{8}\)	\(\frac{1}{2} + \frac{1}{4} + \frac{1}{8}\)
\(\frac{3}{4}\)	\(\frac{1}{2} + \frac{1}{4}\)	\(\frac{2}{9}\)	\(\frac{1}{5} + \frac{1}{{45}}\)
\(\frac{3}{5}\)	\(\frac{1}{5} + \frac{1}{{10}}\)	\(\frac{5}{9}\)	\(\frac{1}{2} + \frac{1}{{18}}\)
\(\frac{4}{5}\)	\(\frac{1}{2} + \frac{1}{4} + \frac{1}{{20}}\)	\(\frac{7}{9}\)	\(\frac{1}{2} + \frac{1}{4} + \frac{1}{{36}}\)
\(\frac{5}{6}\)	\(\frac{1}{2} + \frac{1}{3}\)	\(\frac{8}{9}\)	\(\frac{1}{2} + \frac{1}{3} + \frac{1}{{18}}\)
\(\frac{3}{7}\)	\(\frac{1}{3} + \frac{1}{{11}} + \frac{1}{{231}}\)	\(\frac{4}{9}\)	\(\frac{1}{3} + \frac{1}{9}\)
\(\frac{4}{7}\)	\(\frac{1}{2} + \frac{1}{{14}}\)	\(\frac{5}{9}\)	\(\frac{1}{2} + \frac{1}{{18}}\)
\(\frac{5}{7}\)	\(\frac{1}{2} + \frac{1}{5} + \frac{1}{{10}}\)	\(\frac{5}{9}\)	\(\frac{1}{2} + \frac{1}{{18}}\)
\(\frac{6}{7}\)	\(\frac{1}{2} + \frac{1}{3} + \frac{1}{{42}}\)	\(\frac{{19}}{{20}}\)	\(\frac{1}{2} + \frac{1}{4} + \frac{1}{5}\)

Using the previous table we can add fractions and express such sums; as a sum of unit fractions.

Examples of Heterogeneous Fractions

Example 1

\(\frac{2}{5} + \frac{4}{9} = \left( {\frac{1}{3} + \frac{1}{{15}}} \right) + \left ( {\frac{1}{3} + \frac{1}{9}} \right)\)

\(\frac{2}{5} + \frac{4}{9} = \frac{2}{3} + \frac{1}{{15}} + \frac{1}{9}\)

\(\frac{2}{5} + \frac{4}{9} = \left( {\frac{1}{2} + \frac{1}{6}} \right) + \frac{1 }{{15}} + \frac{1}{9}\)

Example 2

\(\frac{4}{7} + \frac{5}{9} = \left( {\frac{1}{2} + \frac{1}{{14}}} \right) + \left ( {\frac{1}{2} + \frac{1}{{18}}} \right)\)

\(\frac{2}{7} + \frac{5}{9} = 1 + \frac{1}{{14}} + \frac{1}{{18}}\)

Finally, we can express the same fraction as a sum of unit fractions in a different way as:

\(\frac{8}{{63}} = \frac{1}{8} + \frac{1}{{504}}\)

\(\frac{8}{{63}} = \frac{1}{9} + \frac{1}{{63}}\)

\(\frac{8}{{63}} = \frac{1}{{14}} + \frac{1}{{18}}\)