Definition of Mechanical Work

Evelyn Maitee Marin
Industrial Engineer, MSc in Physics, and EdD

From the point of view of physics, mechanical work is the amount of energy that is transferred when a force moves an object through a distance in the direction of that force. It is defined as the dot product of the applied force \(\left( {\vec F} \right)\) and the resulting displacement of the object \(\left( \overrightarrow {Δr} \right)\) in the direction of the force.

The standard unit of measurement for mechanical work is the joule (J), which is equal to the energy transferred when applied a force of one Newton (N) to an object and moves it through a distance of one meter (m) in the direction of the force.

Mechanical work depends on the magnitude of the applied force and the distance the object moves in the direction of the force, so the formula for mechanical work is:
\(W = \vec F \cdot \overrightarrow {Δr} \)

Which is equivalent to:
\(W = F \cdot d \cdot cos\theta \)

where W is the mechanical work, F is the applied force, d is the distance traveled, and θ is the angle between the direction of the force and the displacement of the object.

It is important to mention that the mechanical work can be positive or negative, depending on whether the force is in the same direction as the displacement of the object or in the opposite direction.

The image shows that the man who transports the wheelbarrow with the load is doing a job from the point of view of physics, since most of the force you apply to the wheelbarrow is in the same direction of displacement (horizontal).

Influence of the angle of application of the force in the work

The angle of application of the force has an influence on the mechanical work that is done on an object. In the mechanical work formula W = F x d x cos (θ), the angle θ refers to the angle between the direction of the applied force and the displacement of the object.

If the angle is 0 degrees, it means that the force is applied in the same direction in which it was applied. moves the object, then the mechanical work is maximum and is equal to the force times the distance traveled.

If the angle is 90 degrees, it implies that the force is exerted perpendicular to the direction of motion, then the mechanical work is zero.

For angles less than 90° the work is positive (force in favor of the displacement), and for angles greater than 90° and up to 180°, the work is negative (the force is against the movement).

In general, the smaller the angle between the force and the displacement of the object, the more mechanical work is done. Therefore, the angle of application of the force is an important factor to consider when calculating the mechanical work in a given situation.

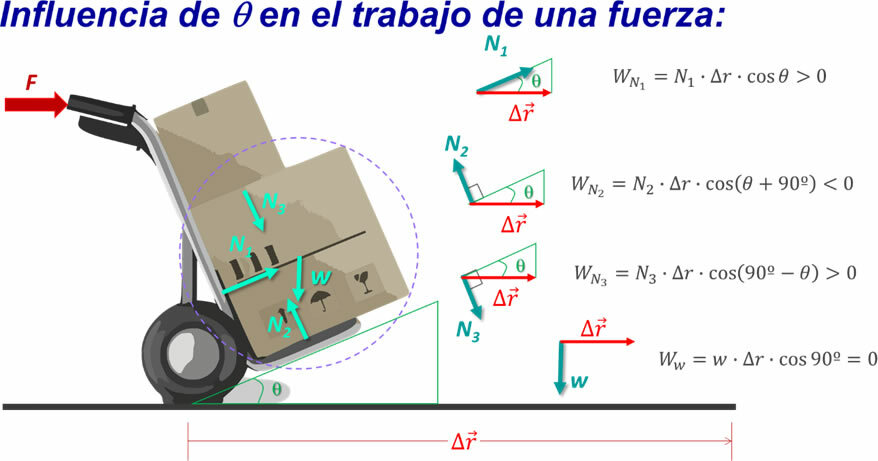
The image shows a wheelbarrow where two boxes are transported. If the larger box (which is located below the second box) is analyzed, it is observed that the forces acting on it are its weight, the two normal exerted on it by the two surfaces of the cart where it rests, and the normal of the second box. On the right side, the work done by each of these forces for the displacement Δr is indicated.

Work done by a variable force

To calculate the work done by a variable force, the displacement of the object can be divided into small equal sections. It is assumed that the force is constant in each section and the work done in that section is calculated using the equation of work for a constant force:

\(W = \vec F \cdot \overrightarrow {Δr} \)

where \(\vec F\) is the force in that section and \(\overrightarrow {Δr} \) is the displacement in that section.

Then, the work done in all sections is added to obtain the total work done by the variable force along the displacement of the object. This method is approximate and may lose accuracy if there are significant variations in force at different points of displacement. In such cases, the calculus of integrals can be used to obtain a more precise solution, especially when the force varies continuously.

\(\sum W = {W_{net}} = \smallint \left( {\sum \vec F} \right) \cdot d\vec r\)

This expression indicates that mechanical work represents the area under the curve on a force versus displacement diagram.

work of a spring

To calculate the work done by a spring, Hooke's law can be used, which states that the force exerted by a spring is proportional to the deformation of the spring; and the constant of proportionality is called the spring constant, represented by the letter k.

The parameters to determine the mechanical work done on a spring are its constant (k) and the magnitude of its deformation (x).

First, both the deformation of the spring (x) and the force exerted by it at each point along the displacement must be measured. Then the work done by the spring in each section must be calculated using the expression:

\({W_R} = \frac{1}{2} \cdot k \cdot {x^2}\)

where k is the spring constant and x is the deformation in that stretch. Finally, the work done in all sections must be added to obtain the total work done by the spring.

It is important to note that the work done by a spring is always positive, since the force and displacement always act in the same direction.

Example of mechanical work

Suppose that an object of mass 2 kg is lifted vertically at a constant speed of 1 meter using a rope. As seen in the following diagram, the force on the string is exerted in the same direction as the displacement of the object toward above and its magnitude is the weight, which is determined as the product of the mass times the gravity, which is 19.62 N (approximately 2 kg x 9.81m/s²).

To find the mechanical work, the expression \(W = F \cdot d \cdot cos\theta \) is applied, where θ is the angle between the direction of the applied force and the displacement of the object, in this case θ = 0° degrees, since both the tension (T) and the displacement go towards above. Therefore, one has:

W = F x d x cos (0) = 19.62 N x 1 m x 1 = 19.62 J

This result indicates that the tension necessary to lift the object against gravity does a mechanical work of 19.62 joules.