What is Regression Analysis, and how is it defined?

Marcoantonio Villanueva Bustamante
Doctor in Psychology

Regression analysis is possibly the most widely used multivariate statistical technique to determine the relationship between one, or a group, of independent variables and a dependent one so that the former can predict the change in the second-

Almost innately, human beings try to give explanations to the events that happen naturally. everyday life, “that person smokes because he or she feels stressed,” “overeating leads to greater body weight”; However, we know that the explanations we give to such events are not always correct. Daniel Kahneman in his book “Thinking Fast, Thinking Slow” describes how, although people tend to make use of all the cognitive elements they possess, they will always make mistakes when trying to explain some event, which is completely normal in a reality where multiple factors coexist. half. So how could we try to explain events as accurately as possible? In the social and health sciences it is possible to do this through data analysis; which is defined as a set of procedures that are helped by statistical techniques descriptive and inferential in order to extract information from an empirical sample of data and develop conclusions. Within data analysis, the technique that will allow us to give reliable explanations to events is a multivariate technique called Regression Analysis.

Regression analysis has a series of variants such as linear regression analysis, multiple regression analysis, logistic regression, mediation analysis, moderation analysis and even structural equation models could be considered (SEM). However, all these variants follow the same operational logic, one or more input variables, which can be known as predictors, independent variables, variables. explanatory or antecedent variables, predict the greatest possible amount of variance of an output variable, which can be known as the dependent variable or simply criterion; When there is more than one Independent Variable, the regression analysis also determines which of these has the greatest influence on the Dependent Variable.

To understand how these relationships occur, we must resort to the following equation, which presents a simple linear regression model:

y = B_either +B_Yo x and

Where,
b_either = Origin of slope
b_Yo = Degree of inclination of the line (slope)
X = VI value
e = Residuals (error)

Simply put, this equation indicates the degree to which the presence of a predictor (independent variable) produces a change in the criterion (dependent variable). It is necessary to mention that although the equation mentions the residual (error) it is not estimated within the model, element for which this technique can be criticized, but that its “evolution” structural equation models (SEM) compensates.

Once the equation has been estimated, it can be visualized using the following two-dimensional plane, called the regression line.

Regression line or slope

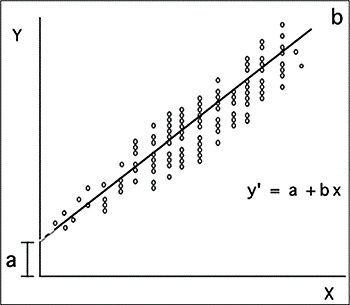
Source: Dagnino (2014)

This graph, in addition to presenting the relationship of the variables involved (through the cloud of points), exposes a line that gives the name to this diagram and indicates the degree to which the empirical data fit the regression value (the value of B).

Although B tells us the degree of the slope, it is actually not very useful for interpretation because It is expressed in the same metric as the variables and, therefore, its values ​​may be too extensive. In this way, by standardizing B based on the Z Scores, the beta coefficient is obtained (β), whose values ​​can be between 0 and 1, both positive and negative and which allows its interpretation. Thus, a negative beta value will indicate that the predictor variable negatively predicts the criterion, that is, the greater the presence of the predictor, the less likely the presence of the criterion; On the contrary, a positive beta indicates that the presence of the predictor favors the presence of the criterion.

Like other inferential statistical techniques, the interpretation of a regression will depend on the hypothesis contrast, or the significance value (p), which in social sciences is typically p > .05.

Finally, an elementary concept of regression analysis is the value of R2 which refers to the variance explained by the model. regression, which can be interpreted directly or by multiplying it by 100 to obtain the percentage of variance explained.

Logistic regression

As mentioned at the beginning, there are different regression analyses. Previously, simple and multiple linear regression was addressed; these assume that both the predictor variables and the criterion are continuous. However, when the variables are not continuous, that is, they are categorical, the logistic regression analysis, this being the only difference with the rest of the regression.