Example of Regular Polygons Area

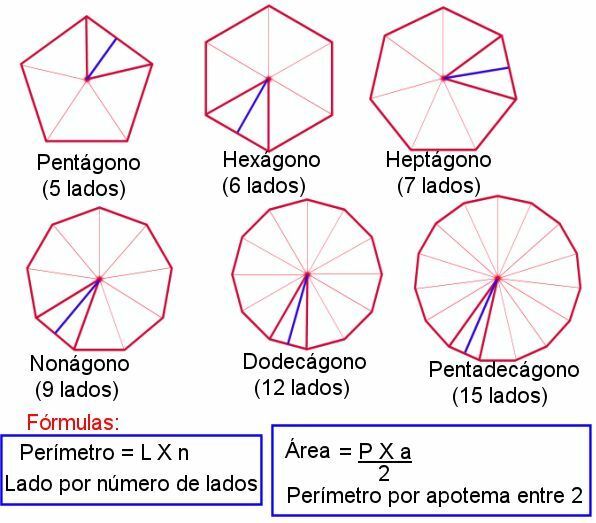
We call the figure a regular polygon that has its equal sides and also its congruent angles, that is, of similar amplitude. So the area of ​​any regular polygon is equal to the sum of the areas of equal triangles into which it can be divided. For example, to achieve the area of ​​any regular polygon we have to multiply its perimeter by the apothem and divide it by two.

We define the apothem as the segment that joins the center of the polygon with the central or midpoint of either side.

The regular hexagon consists of a polygon that has six exactly equal sides and also six equal angles. If we proceed to join the center of it with each of the vertices, all the triangles formed will be equilateral. Therefore, the area of ​​the hexagon will be equal to the area of ​​the six triangles, with the base equal to the side of the hexagon and the height equal to the apothem.

As an example we can say that the formula to find the area of ​​any regular polygon is:

Area = perimeter x apothem
2

The perimeter of any polygon is obtained by multiplying the number of sides by the magnitude or measure of one of them.

Example of regular polygon areas:

1. Regular hexagon of 3 cm of side and 2.6 of apothem

Area = perimeter (3 cm x 6) x apothem (2.6 cm) = 18cm x 2.6cm = 23. 4
2 2

1. Regular pentagon with 2.2 cm side and 2.4 cm apothem

Area = perimeter (2.2 cm x 5) x apothem (2.2 cm) = 11cm x 2.2cm = 12.1
2 2