Example of Improper Fractions

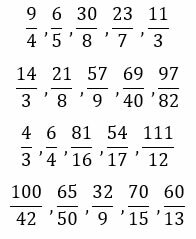
The improper fractions are those whose numerator is greater than the denominator. They are values ​​that exceed unity (the integer: 1), but are still written as a fraction. Recall that the parts of a fraction are:

• Numerator: Number that is placed above, and indicates how many parts (means, thirds, etc.) We are talking.
• Denominator: Number that is placed below, and says into how many parts is it divided the integer. With it we will know if we are talking about means, thirds, fourths, fifths, etc.

Converting improper fractions

Improper fractions are values ​​that, to be easier to handle, can also be expressed as:

• Mixed fractions
• Decimal numbers

Next, the procedures for converting to these two modes will be described.

Converting improper fractions to mixed fractions

An improper fraction can be converted to a mixed fraction in three easy steps:

• I know divide numerator by denominator. We obtain a number with an integer part and a decimal part.
• The whole part (to the left of the decimal point) is put as a whole number of the mixed fraction.
instagram story viewer
• The decimal part, if there is, (from the decimal point to the right) is set as a proper fraction. It is the surplus that was not able to complete the unit.

For example:

In the example above, you get 4 integers, which are equal to 24/6. The original fraction is 25/6, so we have a remainder of 1/6, which is written as is, as a proper fraction.

Converting mixed fraction to improper fraction

When the improper fraction is needed and you have a mixed fraction, follow these steps:

• Multiply the whole part times denominator. This way you will know how many parts (means, thirds, quarters, etc.) are in those integers.
• These parts (means, thirds, fourths) are added to the proper fraction of the problem.

To learn more about proper fractions, visit: Example of proper fractions.

To learn more about mixed fractions, visit: Mixed Fractions Example.

Converting improper fractions to decimal numbers

This conversion is much faster. Just have to divide the numerator by the denominator. The result will be the decimal number, made up of an integer part and a decimal part. For example:

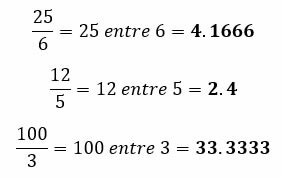
Problem with improper fractions

Both improper fractions and proper fractions make it easier to solve problems involving fractions, because their values ​​are easier to handle than those of mixed fractions.

Problem with fractions:

In a jug with a volume of 4 liters, the following amounts of water are added or removed:

• 2 liters are added
• 1/2 liter is added
• 3/4 liter is withdrawn
• 1/2 liter is added
• 3/4 liter is withdrawn

How much water is left in the jug? In this problem, whole numbers and fractions are used. In addition, operations are carried out with them. You start by expressing this operation:

2 + 1/2 - 3/4 + 1/2 - 3/4

Then, each term is going to be transformed to the common denominator of all. In this case, it is 4. Afterwards, they will be added or subtracted, until reaching the final result.

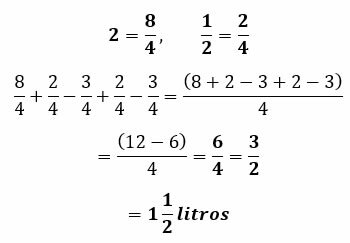
Examples of improper fractions