Decimal Numbers Example

The decimal numbers are those that have a decimal part, that is, a part whose value does not reach a whole number. The decimal part begins to the right of the decimal point, which is what determines where the integer part of the number ends.

For example:

3.141592

The integer part of the number is the digit 3, followed by the decimal point, and all accompanying decimals.

The term "decimal" is based on a system of submultiples of the unit, based on the number 10.

The entire region of the square represents the Unit. If it is divided by 10, we will have a dozen columns, like the one shaded. Each one will represent a Tenth of the Unit. If the columns in turn are divided by 10, we will have a small square, like the one in the corner. This small square will represent one Hundredth of the Unit. Thus, successively, we will find the Thousandths, which are one-tenth of the Hundredths, and the Ten-thousandths, which are in turn one-tenth of the Thousandths.

The above explanation is useful to define the position of each digit in the example number:

3.141592

We know that 3 corresponds to the position of the Units, which are whole numbers. From the decimal point to the end on the right, the entire part that does not reach to complete a Unit is found.

In turn, the decimal part has an order in the digits that make it up:

3.141592

The first number 1 is in the first position, representing the Tenths that are not able to become units. To its right is a 4, represented by the Hundredths that did not reach a tenth. It is followed by 1 of the thousandths, 5 of the ten thousandths, 9 of the hundred thousandths, and 2 in the millionths.

Example:

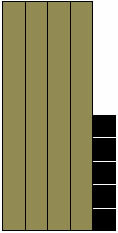
We find a complete Unit, and 4 Tenth columns and five Hundred frames are added. This number, as a result, will be represented:

1.45

Periodic Decimal Numbers

There are operations in which the results are decimal numbers that are made up of a repetitive sequence, without reaching an end. Such is the example of:

10/3 = 3.3333333333333…

10/9 = 1.1111111111111…

Where the result will never be exact. It is an indeterminacy. The way to represent them on paper is by adding a horizontal line to the last written digits.

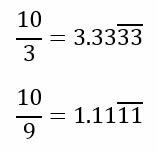
These are called Periodic Numbers.