Radical Simplification Example

Expressions of the form bⁿ they represent us a unique number, which we call the nth principal root of b and as mentioned before there is cases where it is more advantageous to express the quantity with a radical rather than using exponents fractional.

The laws of radicals follow from the already generalized laws of exponents, and it is necessary to keep them in mind when working with radicals. Remember that

bⁿ = b 1 / n and if n is even ⇒ b> 0

Taking advantage of these laws of radicals, the radical form can be changed in the following ways:

a) Remove the multiple powers of the index from the radicand, for which we factor before.

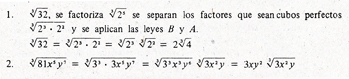
b) Reduce the index of the radical, without forgetting that the radicand must be positive.

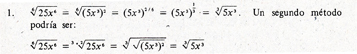
c) Rationalize the denier. Rationalizing means replacing the expression with an equivalent without a radical where indicated.

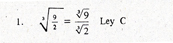
We look for a factor (z) such that it makes the radicand in the denominator have a multiple exponent of the index of the radical and using the theorem x / y = xy / yz the product is made.

RADICAL SIMPLIFICATION EXAMPLE: