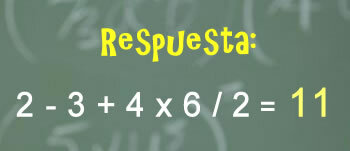Example of Order of Operations

The order of operations It is one that is used to perform calculations in a mathematical expression, which includes different mathematical operations. A hierarchical order is established on which mathematical operations must be solved first to arrive at the result of a mathematical equation.

The steps in the order of operations are:

1.  Mathematical problems that are framed within the following symbols () [] {}, or within some other symbol, are solved first.
2. Then problems such as Square roots or Powers are solved (they are also called Indices or Exponents).
3. The next step is to solve the Multiplication or Division problems that are presented in the equation. (This is done from left to right)
4. Finally, the Additions and Subtractions that appear in the equation are solved (this is done from left to right).

If any calculation mentioned in the previous list is missing, just skip that step, and continue with the next steps according to the hierarchy.

Example of order of operations:

The order of operations can be observed in the following equation:

2 - 3 + 4 x 6/2 =?
The priority of the operations is the grouping signs parentheses (), square brackets [], braces {}, and top bar first.
The second place in priority is the powers and roots.
The next level multiplication and division.
Finally add and subtract.
The different terms of the equation are solved from left to right.

In this example
2 - 3 + 4 x 6/2 =?

Step 1
Since we have addition, subtraction, multiplication and division, we will first carry out multiplication and division, doing them from right to left:
TO. The first operation from left to right is the 4x6 multiplication, which we will indicate in parentheses and solve:
2 -3 + (4 x6) / 2 = 2 - 3 + 24/2.
B. The next operation is the division by 2 of the result of the previous multiplication, that is, 24, which will be the next operation we will perform:
2 -3 + (24 /2) = 2-3 +12.

Step 2
Now we will carry out the additions and subtractions of the same order from right to left:
TO. The first operation is the subtraction of 2-3 that we will put in parentheses and solve:
(2-3)+ 12 = -1 +12.
B. To finish we will do the final operation:
-1 +12 =11.
The result of:
2 - 3 + 4 x 6/2 = 11