Relative Motion Example

The relative motion is the one that is assumed in a body moving within a frame of reference, which moves within another frame of reference. To better understand it, the concepts of reference frames will be established, which can be inertial or non-inertial.

A frame of reference is the set of bodies with respect to which the movement is described. Systems such that in them the Law of Inertia is verified, that is, Newton's Laws of Motion, are called Inertial Systems. Any system that moves smoothly with respect to an inertial system is therefore also inertial.

An object free of forces that affect it is posed, which moves with a velocity v with respect to a inertial system K, and it is assumed that another system K 'translates with respect to K with a constant speed V. Since it is known that no forces act on the object and the system K is inertial, the velocity v will remain constant. The free object will move with uniformity also with respect to the K 'system, and consequently this system is also inertial.

When analyzing the free motion of a body, you cannot differentiate between the various inertial systems. From experience it is pointed out that all the laws of mechanics are the same in all inertial systems, and this fact is called "Galileo's Principle of Relativity".

In practice, Galileo's Principle of Relativity means that the Observer located inside a closed room is not able to distinguish if the room is at rest or is moving with speed constant; however, you can tell the difference between smooth motion and accelerated motion.

Examples of Relative Motion

Systems in accelerated rectilinear motion

A Reference system K 'that moves with a variable speed V (t) (this speed is a function of time) will be taken into account, with respect to an inertial system K. According to the principle of inertia, an object free of forces is going to move with a constant speed v with respect to the system K. The velocity v of the object with respect to the accelerated system K 'verifies the Galilean sum of velocities:

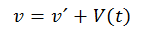
Consequently, v 'cannot be constant. This means that in the system K 'the law of inertia is not fulfilled, since with respect to K' an object free of forces does not have uniform motion. Finally, K 'is a non-inertial reference frame.

It will be assumed that, at a given instant, the acceleration of system K 'with respect to system K is A. Since a free object keeps its speed constant with respect to the inertial system K, with respect to the system K 'it will have an acceleration a' = -A. Of course, the acceleration that an object acquires with respect to the system K 'will have an acceleration that is independent of the properties of the object; specifically, a 'does not depend on the mass of the object.

This fact makes it possible to establish a very important analogy between motion in a non-inertial system and motion in a field. gravitational field, since in a gravitational field all bodies, without depending on their mass, acquire the same acceleration, calculated in 9.81 m / s² for terms of planet Earth.

The laws of mechanics do not hold in an accelerated system. However, the dynamic equations can be altered so that they are also valid for the motion of an object with respect to a non-inertial system K '; it is enough to introduce an Inertial Force F *, proportional to the mass of the body and to the acceleration –A acquired with respect to K´ if it is free of interactions.

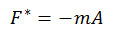
It is important to note that the Inertial Force F * differs from forces related to interactions in two respects: First of all, there is no Force –F * to counteract it to balance the system. And secondly, the existence of this inertial force is dependent on the system considered. In the inertial system Newton's Law for a free object is:

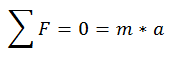
But for the accelerated reference system it is stated:

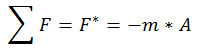
Rotating Reference Systems

We will consider a body that describes a circle of radius r with constant velocity v, taken with respect to an inertial system K. With this reference, the body will have an acceleration, which is equivalent to:

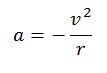
This if the change in r, from the center of the circumference outwards, is assumed to be positive. With respect to a K 'system whose origin coincides with the center of the circumference and which rotates with an angular velocity Ω, the body has a tangential velocity v´T + Ωr, and its acceleration is:

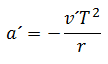
Then, between the acceleration of the body with respect to K 'and the acceleration with respect to K there is a difference:

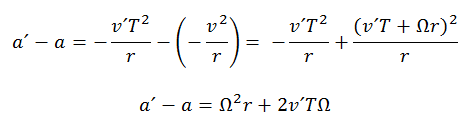
This difference in accelerations between both systems can be explained by the existence in the system K 'of an inertial force:

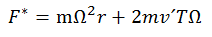
Complemented with "m", the mass of the body, to resemble Newton's second law, and depends on the distance from the body to the center of the circumference and its tangential velocity v'T with respect to the system rotary K´. The first term corresponds to a radial force that points from the inside out, and is called the Centrifugal Force;the second term corresponds to a radial force pointing outward or inward, according to the positive or negative sign of v´T, and it is the so-called Coriolis force for a body that moves tangentially with respect to K´.

10 examples of Relative Movement in daily life:

1. The translational movement of the Earth, with respect to that of the other planets, whose central point is the Sun.

2. The movement of a bicycle chain relative to that of the pedals.

3. The descent of an elevator in a building, with respect to another that is ascending. They appear to go faster, because between them they enhance the optical illusion of the other's movement.

4. Two racing cars going into close positions during a competition appear to be moving very little to each other, but when the perspective is placed on the entire track, you can see the actual speed at which they travel.

5. Athletes in a marathon are grouped in a crowd, so a group speed is discernible but not a single speed, until the perspective is focused on it. Its acceleration is better appreciated when compared to a previous competitor.

6. When the study of a fertilization process is carried out, the micrometric velocities of the spermatozoa bound for the ovule are captured, as if they were macroscopic velocities. If natural speeds were to be observed with the human eye, they would be imperceptible.

7. The displacement of the Galaxies in the Universe is on the order of Kilometers every second, but it is undetectable by the vastness of space.

8. A space probe can register its own velocity such that on the Earth's surface it would be enormous, but observing it in space magnitudes, it is slow.

9. The hands of the clock also apply to the concept of relative motion, because while one is moves at the rate of one space every second, another moves one space every minute, and the last one space each hour.

10. Power poles appear to be going at speed when viewed from inside a moving car, but they are actually at rest. It is one of the most representative examples of relative motion.