Coulumb's Law Example Example

The Coulumb's Law, also known as the Law of Electric Charges, it is a law of electrostatics that consists of the discovery that the charges with the same sign repel and charges with the opposite sign attract. Columb's law was discovered by the french scientist Carlos Agustín de Coulumb in 1795. The discovery came after observing how an electrically charged sphere reacted in a torsion balance, moving away or approaching, when another sphere also with charge approached it electrical. The electrical charges were passed to the spheres by rubbing a rod on different materials, such as wool, silk and other fibers.

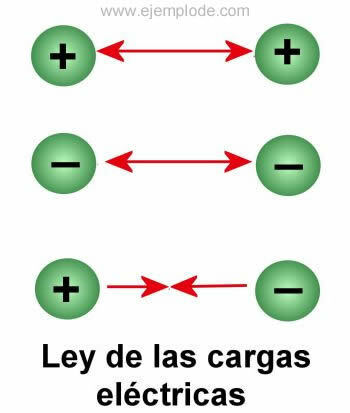
As a consequence of his observations, he realized that when two electric charges with the same sign interact, that is both are positive or both are negative, they tend to separate, that is, they repel and when the charges are of the opposite sign they attract. He also realized that the force with which they attract or repel each other is in relation to the electric charge and the distance at which the charges are. He stated it as follows:

The attractive or repulsive force between two electric charges is directly proportional to the electric charge and inversely proportional to the square of the distance that separates them.

This means that the greater the charge, the greater the force with which they attract or repel each other, and the more distance there is between the charges, the lower the attractive force.

Another factor that influences the force of attraction is the surrounding environment, since the electrical conductivity varies depending on the environment. This value of the conductivity of the medium is called the dielectric constant.

The attractive or repulsive forces are calculated with the following formula:

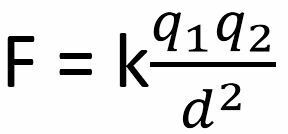
The values ​​are as follows:

F: is the force that we are going to calculate.

k: is the dielectric constant, that is, the conductivity of the medium that surrounds the electric charges. For air and vacuum, its value is 9 X 10⁶ N m²/ C².

what₁, what₂: They are the electrical charges to consider, averages in Coulumbs. The Coulumb is the measure of electrical charge, which can have a positive or negative value. The value of a Coulumb is 6.241509 X 10¹⁸ electrons. If the value is negative (negative charge), it means that its charge can give up electrons. If its value is positive (positive charge), it means that it can absorb electrons. Charges are generally measured in submultiples, such as milliCoulumbs (mC) or microCoulumbs (mC)

d: is the distance between the charges, measured in meters. They can also be measured in submultiples, such as centimeters (cm), millimeters (mm), or microns or micrometers (mm).

Examples of Coulumb's Law calculation:

Example 1: If we have two electric charges of 5mC and 7mC, separated by 3mm, determine if they are going to attract or repel each other, and calculate the force with which they do so.

As the two charges are positive, that is, of the same sign, they will repel each other (charges of the same sign attract).

Now we write down the values ​​that we will substitute in the formula We will substitute the submultiples for powers of the form 10^x, to simplify the calculations:

k = 9 X 10⁹ N m²/ C²
what₁ = 5 mC = 5 X 10^-3 C
what₂ = 7 mC = 7 X 10^-3 C
d = 3mm = 3 X 10^-3 m

Now we carry out the operations, starting with the multiplications of the second member:

(what₁) (what₂) = (5 X 10^-3) (7 X 10^-3) = 35 X 10^-6 C
d² = (3 X 10^-3)² = 9 X 10^-6

We make the division:

(35 X 10^-6) / (9 X 10^-6) = 3.88 X 10⁰ = 3.88

We multiply the result by the constant:

(9 X 10⁹) (3.88) = 34.92 X 10⁹ N

Example 2: Calculate the distance between the charges, if we know that there is an attractive force of -25 X 10⁵ N and the charges are 2mC and -4mC.

In this example, since we know the values ​​of F and k, what we must do first is divide F by k, to find out how much is the value of [(q₁) (what₂)] / d²:

-25 / 9 = -2.77 X 10^5-9= 2.77 X 10^-4

We already know that the value of [(q₁) (what₂)] / d² is 2.77 X 10^-4

Now we are going to divide this result by the value of the charges.

(what₁) (what₂) = (2 X10^-3) (- 4 X 10^-3) = -8 X 10^-6

Now we divide 2.77 X10^-4 between -8 X 10^-6

2.77 X10^-4 / -8 X 10^-6 = 0.34625 X10² = 34.625

Recall that this result is d², so we must calculate the square root to obtain the distance in meters:

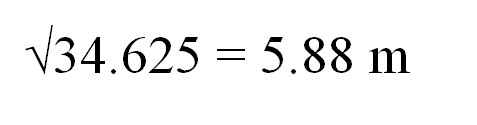
Do not forget to leave your comments.